ByteTrack (01) - 논문 리뷰 part 1

ECCV 2022. [Paper] [Github]
Zhang, YiFu, et al.
Huazhong University of Science and Techonology
7 Apr 2022

Introduction

논문의 제목은 ByteTrack: Multi-Object Tracking by Associating Every Detection Box 이다.
논문을 다 읽은 후에는 이 말이 무슨 의미인지 알 수 있다.
모든 detection box를 associating하면서 tracking을 하는 논문인가? 정도로 예상하고 넘어가자.

이 논문은 object tracking에 대한 논문으로 object tracking이란 움직이는 객체를 탐지하고 객체의 움직임을 추적하는 것이다.
또한 tracking은 YOLO와 같은 detector가 예측한 박스를 기반으로 tracking을 수행한다. 이를 tracking by detection이라 한다.

Object tracking에는 많은 접근법이 있으며 몇 가지만 간략하게 소개하자면 먼저 박스 간의 임베딩을 비교하는 방법이 있을 수 있겠다.(ex. cosine similarity) DeepSORT, FairMOT와 같은 논문이 이에 해당한다. 다른 방법으로는 attention 기반의 방법이 있다. 이는 transformer 기반 detector 전용 알고리즘이며 transtrack, MOTR이 이에 해당한다. 또 다른 방법으로는 IOU 기반의 방법이 있다. 이는 box의 IOU를 계산하여 tracking하고자 하는 알고리즘으로 ByteTrack, BoT-SORT, SparseTrack 등이 해당한다. 물론 IOU 기반 방법과 임베딩 기반 방법(Re-ID)를 결합하기도 한다.

Background

ByteTrack을 이해하기 위해서는 어느 정도의 배경 지식이 필요하다. 특히 ByteTrack의 근간이라 할 수 있는 SORT논문을 보고 온다면 좋다.

칼만 필터(Kalman filter)

Tracking의 수행에는 기본적으로 이전 프레임에서 검출된 객체는 다음 프레임에도 비슷한 위치에 존재한다는 가정이 있다.
이전 프레임의 detection과 다음 프레임의 detection을 비교하는 것은 극히 직관적인 생각이다. 여기에 더해 tracking의 정확도를 높이기 위해 칼만 필터라는 것을 사용한다.
칼만 필터는 이전 스텝의 state를 기반으로 다음 state를 예측하며 추정값은 예측값과 측정값에 적절한 가중치를 부여한 후 더해서 계산하고 가중치(Kalman gain)은 매번 새로 계산하는 형태이다. 칼만 필터는 살짝 난해한 내용이기 때문에 자세한 이해에는 칼만 필터는 어렵지 않아라는 책을 참고하자.
Object tracking에서는 x,y,a,h,vx,vy,va,vh를 이용하여 다음 state를 예측한다. 여기에서 (x,y)는 박스의 중심 좌표이고 a는 aspect ratio(w:h), h:높이에 해당하고 앞에 붙은 v는 속도에 해당한다. 즉 현재 박스의 위치와 크기, 속도를 이용해 다음 박스의 위치와 크기를 예측한다고 보면 되겠다. 여기에서 w를 쓰지 않고 왜 a를 사용하냐라는 의문이 들 수 있는데 의미상으로는 이미지 크기나 위치 등에 변할 수 있는 다른 state와 달리 상대적인 비율을 나타내는 a를 통해 객체의 형태를 유지하면서 tracking을 진행하고자 하는 것이며 당연히 w로 교체가 가능하다. 이론적으로는 h에 비해 w의 변화에 상대적으로 취약하다.

헝가리안 알고리즘(Hungaian algorithm)

Tracking이란 객체의 id를 유지하면서 추적하는 것이다. 다양한 object에 대해 매칭이 필요한데 하나의 obect에서 하나의 object로 연결되므로 할당 문제(assignment problem)으로 문제를 해결하려고 한다. 헝가리안 알고리즘은 할당 문제의 최적화 기법이다. 즉 여러 개의 박스를 어떻게 다 비교하여 매칭할 것인가? 박스는 1대1 매칭이 되어야 하니 할당 문제로 해결하면 빠르게 매칭을 시킬수 있겠네? 이런 느낌이다.
아래의 그림을 통해 헝가리안 알고리즘을 살펴보자.

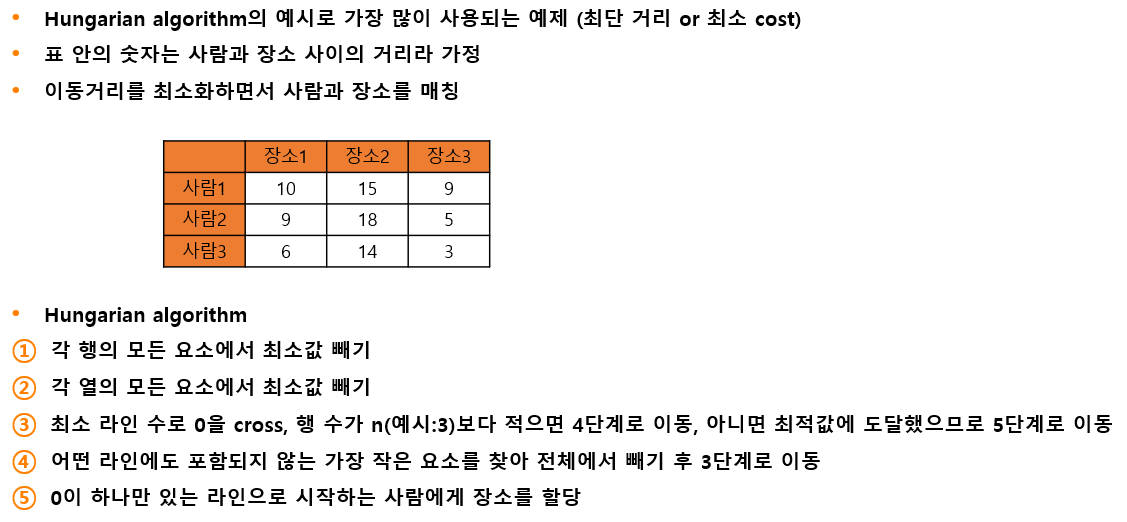
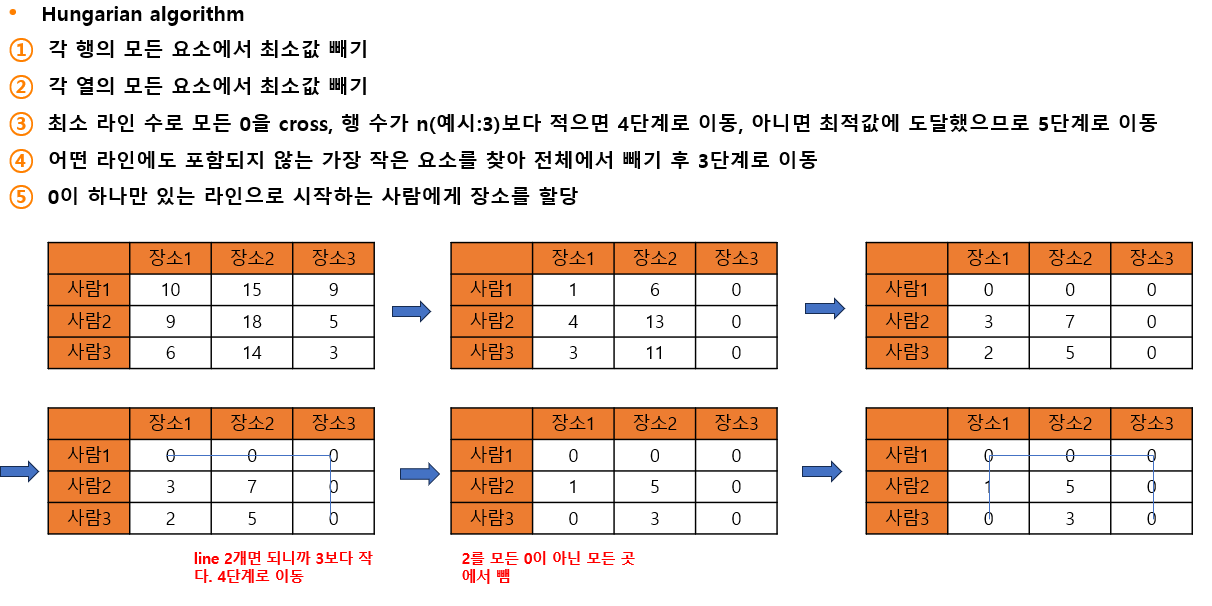
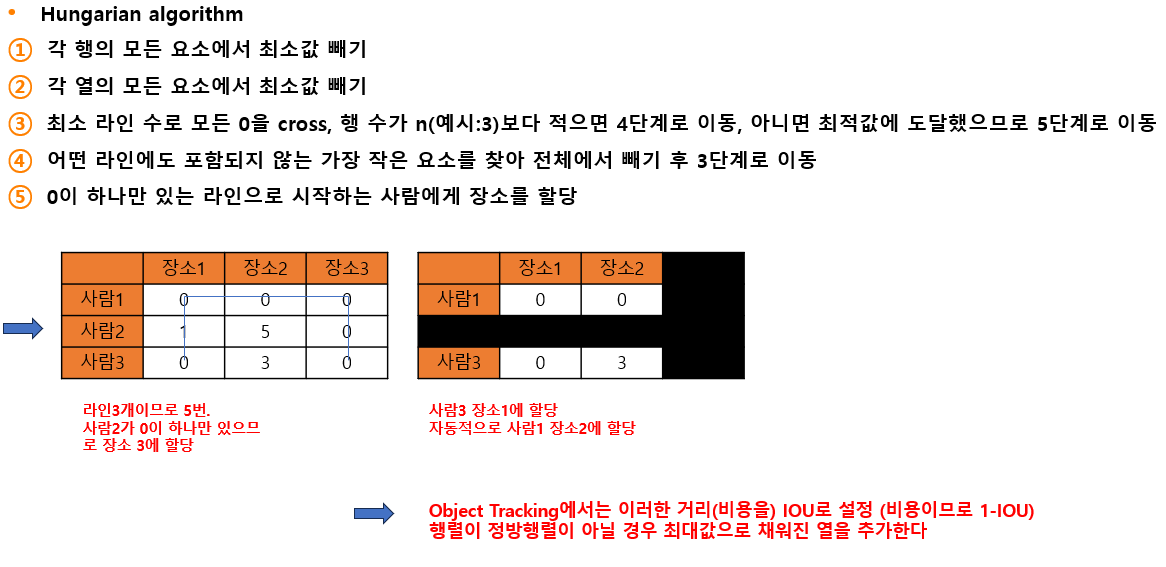
실제 코드에서는 헝가리안 알고리즘을 구현하여 사용하지는 않고 lap.lapjv (Linear assignment problem; 선형할당문제 라이브러리, Jonker-Volgenant; 헝가리안 알고리즘 변형)를 사용한다.

코드를 가져와서 그림의 예제를 실험해보자.

import numpy as np
import time

def linear_assignment(cost_matrix):
    try:
        import lap  # linear assignment problem solver
        _, x, y = lap.lapjv(cost_matrix, extend_cost=True)
        return np.array([[y[i], i] for i in x if i >= 0])
    except ImportError:
        from scipy.optimize import linear_sum_assignment
        x, y = linear_sum_assignment(cost_matrix)
        return np.array(list(zip(x, y)))

# 예제 cost_matrix
cost_matrix = np.array([[10, 15, 9], [9, 18, 5], [6, 14, 3]])

st = time.time()
result = linear_assignment(cost_matrix)
et = time.time()

# 결과
print('result:')
print(result)
print('elapsed:',et-st)

result:
[[0 1]
 [1 2]
 [2 0]]
elapsed: 0.00048232078552246094

Tracking에서의 헝가리안 알고리즘은 detection과 prediction을 매칭하는 것이며 cost는 similarity를 사용한다. IOU 기반의 방법에서는 IOU를 비용으로 처리해야 하기 때문에 $1 - IOU$를 사용할 것이다.

---

ByteTrack에 대한 배경 지식 설명은 여기에서 마치고 다음 포스팅에서 ByteTrack의 원리와 실험 결과를 설명하고자 한다.