Marching Cubes 알고리즘

2026-02-03 1 분 소요

Marching Cubes 알고리즘은 3D 공간 각 지점에서의 밀도 값을 이용하여 연속적인 표면(iso-surface)를 다각형 메쉬(보통 삼각형)로 추출하는 알고리즘이다.

아이디어는 어렵지 않다.

1. 3D 공간을 작은 큐브(정육면체)로 쪼갠다. (voxel grid)

2. 각 큐브의 8개 꼭짓점 값을 기준값(isovalue)과 비교한다.

3. 8개의 꼭짓점 조합에 따라 표면이 어떻게 지나는지를 미리 정의해둔 lookup table로 찾는다.

8개의 꼭짓점은 0,1의 값을 가질 수 있으므로 총 2^8 = 256개의 경우가 존재한다.
아래의 그림은 좌측 하단의 꼭짓점을 기준으로 발생할 수 있는 고유한 모양의 케이스를 나타는데 제외하면 해당 모양으로 대칭이다. (모든 꼭짓점 포함도 존재하나 빈 것과 대칭으로 본 듯 하다)

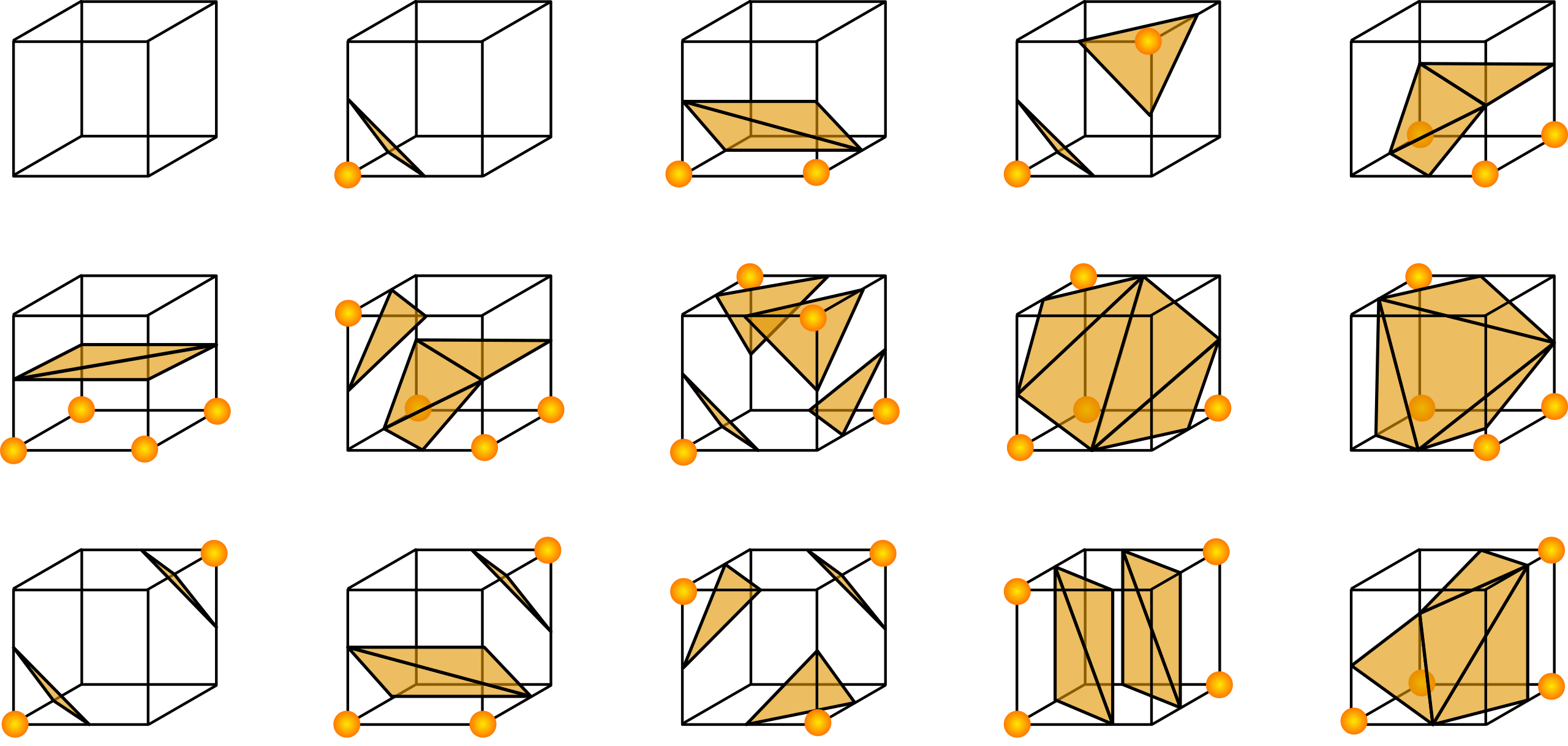
Marching cubes lookup table cases

4. 표면이 실제로 지나가는 edge를 linear interpolation으로 계산한다.

5. 생성된 다각형들을 합쳐 전체 표면 메쉬를 만든다.

이미지로부터 3D를 생성하는 연구들의 경우 단일 이미지로부터 3D SDF를 예측하고 marching cubes기반 알고리즘으로 메쉬를 추출한다. (marching cubes 원 알고리즘 자체는 한계가 있으므로 FlexiCubes와 같은 개선된 알고리즘을 사용한다.)

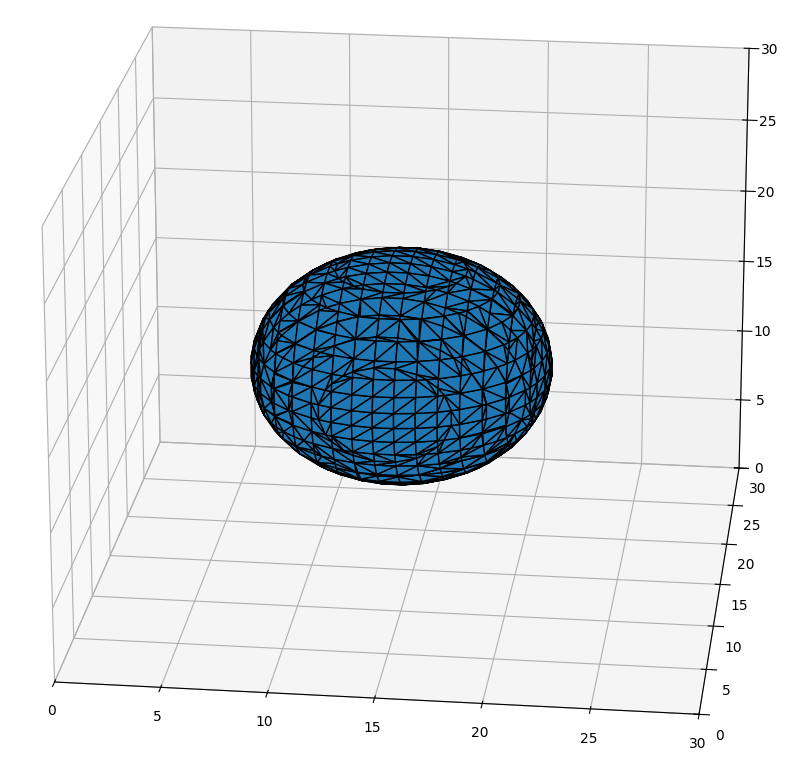
ex) 반지름이 5인 구

Sphere example with marching cubes

Marching Cubes의 2D 버전은 Marching Squares라 부른다.

만약 Marching Cubes가 어렵다면 2D 버전을 먼저 이해하면 똑같이 3D로 확장하면 된다. 2D에서는 꼭짓점이 4개이므로 경우의 수는 16개이고 이 lookup table을 미리 정의한다.

자세한 설명은 https://en.wikipedia.org/wiki/Marching_squares 를 참고하자.

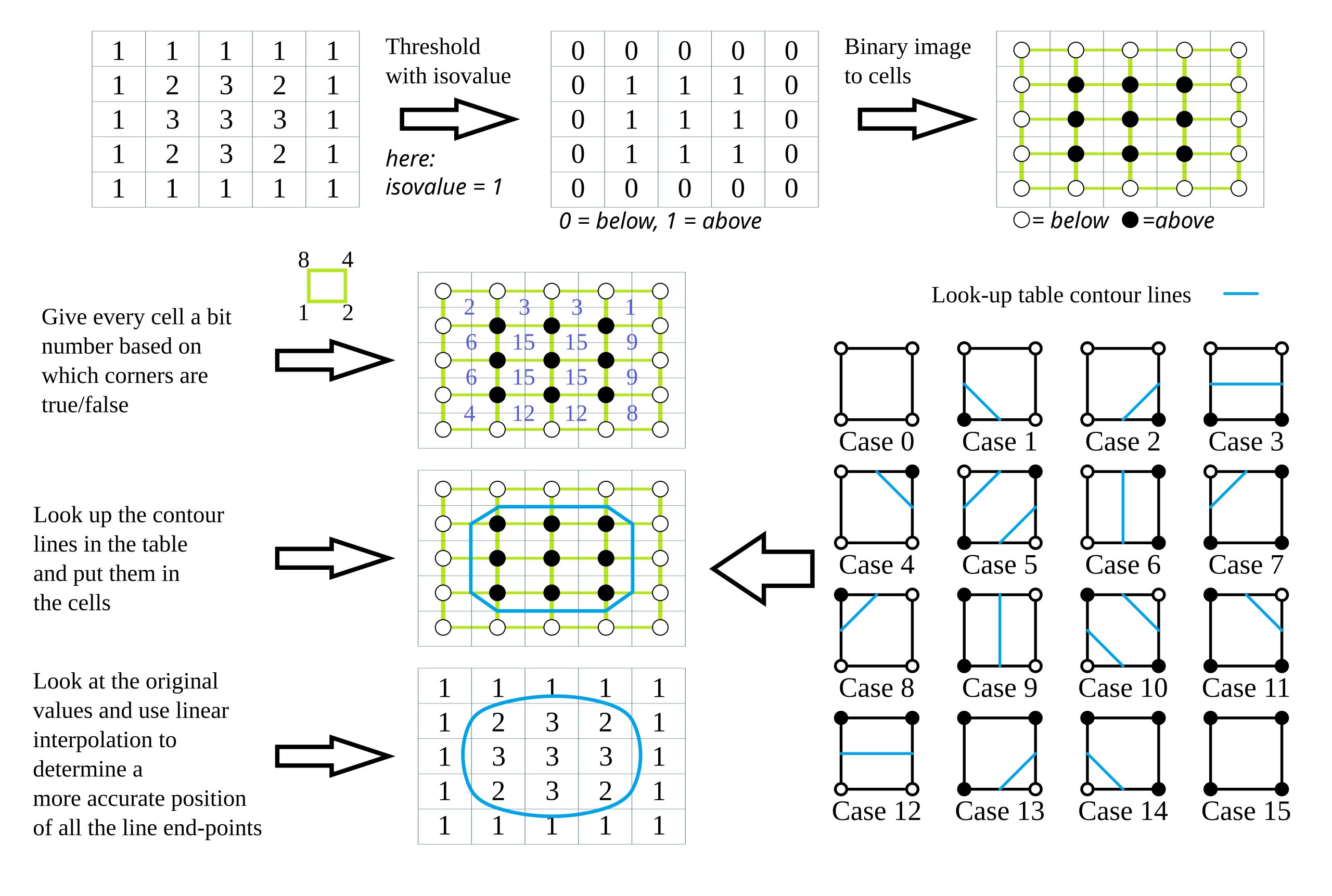
Marching squares cases

마지막 파란색 원 형태는 실제로 이렇다는 것은 아니고 실제로는 lookup table에 정의된 것처럼 직선 모양이다. 하지만 셀이 많아지면 원형처럼 보이게 된다는 것을 강조한 것으로 보인다.

참고