10 분 소요

Introduction

Denoising Diffusin Probabilistic Models(DDPM)는 GAN과 같은 adversarial network를 사용하지 않고도 고품질의 이미지를 생성하는 데에 성공했다. 하지만 markov chain에 기반하기 때문에 샘플링 과정에서 많은 시간이 소요된다. (1000 step이면 reverse process가 노이즈로부터 1000step이 진행되어야 1장의 이미지가 생성되기 때문이다.) 이 DDIM의 핵심 contribution은 forward process를 non-markovian process로 일반화하고 그에 따라 reverse process 역시 non-Markovian process로 만들었다는 것이다. 결과적으로 샘플링 속도를 DDPM대비 10~50배 개선했다고 주장한다.

Background

이 논문은 DDPM을 기반으로 하기 때문에 이에 대한 이해가 필요하다. 자세한 내용은 DDPM에 관련 리뷰 를 참고하는 것을 권장한다.

데이터의 분포 $q(x_0)$가 주어질 때, $p_\theta(x_0)$ 가 $q(x_0)$를 근사하는 것을 목표로 학습한다.

\[p_\theta(x_0) = \int p_\theta(x_{0:T}) \, dx_{1:T}, \quad \text{where} \quad p_\theta(x_{0:T}) := p_\theta(x_T)\prod_{t=1}^{T} p_\theta^{(t)}(x_{t-1}\mid x_t)\]

파라미터 $\theta$는 variational lower bound를 최대화하는 방향으로 학습한다. $x_t$에서 $x_0$로 샘플링하는 과정은 generative process라 한다. (DDPM 원 논문은 -log 형태로 upper bound를 최소화하는 방향으로 설명하였다. 아래 수식의 부등호를 빨갛게 한 것은 논문에 제시된 수식의 부등호 방향은 반대로 되어있는데 오류라 생각되기 때문이다.)

\[\max_{\theta} \mathbb{E}_{q(x_0)} \big[ \log p_\theta(x_0) \big] {\color{red}\ge} \max_{\theta} \mathbb{E}_{q(x_0, x_1, \ldots, x_T)} \big[ \log p_\theta(x_{0:T}) - \log q(x_{1:T} \mid x_0) \big]\]

$q(x_t \mid x_{t-1})$을 forward process라 하고 평균과 분산은 $\alpha_t$, $\alpha_{t-1}$로 표현된다. 여기에서 $a_t$는 DDPM에서의 $\bar \alpha_t$ 로 joint에 해당한다.

\[q(x_{1:T} \mid x_0) := \prod_{t=1}^{T} q(x_t \mid x_{t-1}), \quad \text{where} \quad q(x_t \mid x_{t-1}) := \mathcal{N} \left( \sqrt{\frac{\alpha_t}{\alpha_{t-1}}}\, x_{t-1}, \left(1 - \frac{\alpha_t}{\alpha_{t-1}}\right) I \right)\]

forward process를 다음과 같이 정의할 수 있었다.

\[q(x_t \mid x_0) := \int q(x_{1:t} \mid x_0)\, dx_{1:(t-1)} = \mathcal{N} \left( x_t; \sqrt{\alpha_t}\, x_0, (1 - \alpha_t) I \right)\]

$x_t$는 $x_0$와 노이즈 $\epsilon$의 선형 결합으로 표현할 수 있다.

\[x_t = \sqrt{\alpha_t}\, x_0 + \sqrt{1 - \alpha_t}\, \epsilon, \quad \text{where} \quad \epsilon \sim \mathcal{N}(0, I)\]

$\alpha_t$가 충분히 0이 가까워지면 $q(x_t \mid x_0)$ 은 임의의 $x_0$에 대해 표준 가우시안 분포로 수렴한다. 따라서 자연스럽게 generative process가 표준 가우시안 분포를 따른다고 설정할 수 있다.

\[p_\theta(x_T) := \mathcal{N}(0, I)\]

학습 가능한 평균 함수와 고정된 분산을 갖는 가우시안으로 모델링할 경우 objective equation은 아래와 같이 단순화할 수 있다.

\[L_\gamma(\epsilon_\theta) := \sum_{t=1}^{T} \gamma_t \mathbb{E}_{x_0 \sim q(x_0),\, \epsilon_t \sim \mathcal{N}(0, I)} \left[ \left\| \epsilon_\theta^{(t)} \left( \sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t}\, \epsilon_t \right) - \epsilon_t \right\|_2^2 \right]\]

여기에서 $\epsilon_\theta$는 T개의 함수 집합이며, 각 함수 $\epsilon_\theta^{(t)} : \mathcal{X} \rightarrow \mathcal{X}$ 는 학습 가능한 파라미터 $\theta^{(t)}$ 를 가진다.

\[\epsilon_\theta := \{\epsilon_\theta^{(t)}\}_{t=1}^{T}\]

또한 $\gamma := [\gamma_1, \ldots, \gamma_T]$ 는 목적 함수에서 사용되는 양수 계수 벡터이며 이는 $\alpha_{1:T}$에 의존한다. DDPM에서는 generation 성능을 최대화하기 위해 $\gamma$ 를 1로 설정하였다.

DDIM 설명

DDPM vs DDIM forward process

생성 모델에 필요한 iteration 수를 줄이기 위해 inference(diffusion) process를 다시 한번 생각해 볼 필요가 있다. Key observation은 DDPM의 목적함수 $L_r$가 marginal 분포(주변확률분포, 특정 확률변수만의 확률분포) $q(x_t \mid x_0)$에만 의존하고 joint 분포 $q(x_{1:T} \mid x_0)$에는 직접적으로 의존하지 않는다는 것이다. 그래서 Figure 1의 우측 그림과 같은 non-Markovian process를 도입하려고 하는 것이다. 이러한 process는 DDPM과 동일한 목적 함수를 가짐을 보일 수 있다.(아래에서)

Non-Markovian forward process

실수 벡터 $\sigma \in \mathbb{R}_{\ge 0}^{T}$ 에 대하여 아래의 수식을 살펴보자.

\[q_\sigma(x_{1:T} \mid x_0) := q_\sigma(x_T \mid x_0) \prod_{t=2}^{T} q_\sigma(x_{t-1} \mid x_t, x_0)\] \[\text{where \quad} q_\sigma(x_T \mid x_0) = \mathcal{N} \left( \sqrt{\alpha_T}\, x_0, (1 - \alpha_T) I \right)\]

아래는 논문의 7번 수식으로 모든 $t$에 대해 $q_\sigma(x_t \mid x_0) = \mathcal{N}(\sqrt{\alpha_t}\, x_0, (1 - \alpha_t) I)$ 를 만족시키기 위해 평균 함수를 아래와 같이 구성한다.

\[q_\sigma(x_{t-1} \mid x_t, x_0) = \mathcal{N} \left( \sqrt{\alpha_{t-1}}\, x_0 + \sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot \frac{x_t - \sqrt{\alpha_t} x_0}{\sqrt{1 - \alpha_t}}, \, \sigma_t^2 I \right), \quad t > 1\]
  • TMI

어떻게 이 식이 나오게 되었을까 생각해보자.

\[x_t = \sqrt{\alpha_t}\, x_0 + \sqrt{1 - \alpha_t}\, \epsilon_t, \quad \text{where} \quad \epsilon \sim \mathcal{N}(0, I)\] \[x_{t-1} = \sqrt{\alpha_{t-1}}\, x_0 + \sqrt{1 - \alpha_{t-1}}\, \epsilon_{t-1}\]

여기서 $x_{t-1}$을 생성할 때 사용하는 노이즈의 분산 $(1-\alpha_{t-1})$ 을 두 부분으로 나눈다.

  • $A^2$ ($x_t$ 노이즈 재사용)
  • 새롭게 추가되는 무작위 노이즈 $\sigma^2_{t}$

분산의 합이 $1-\alpha_{t-1}$ 이 되어야 하므로

\[A = \sqrt{1 - \alpha_{t-1} - \sigma_t^2}\]

$x_{t-1}$ 은 평균 + A + 랜덤의 형태이므로 다시 쓰면

\[x_{t-1} = \sqrt{\alpha_{t-1}} x_0 + \sqrt{1 - \alpha_{t-1} - \sigma_t^2}\,\epsilon_t + \sigma_t \epsilon\]

여기에서 $\epsilon_{t}$를 아래와 같이 정리할 수 있고

\[\epsilon_t = \frac{x_t - \sqrt{\alpha_t} x_0}{\sqrt{1 - \alpha_t}}\]

이를 대입하면

\[x_{t-1} = \sqrt{\alpha_{t-1}} x_0 + \sqrt{1 - \alpha_{t-1} - \sigma_t^2} \left( \frac{x_t - \sqrt{\alpha_t} x_0}{\sqrt{1 - \alpha_t}} \right) + \sigma_t \epsilon\]

결과적으로 논문의 식을 도출할 수 있다. 분산을 동일하게 설정하기 위해 역으로 맞춘 느낌이다.

\[q_\sigma(x_{t-1} \mid x_t, x_0) = \mathcal{N} \left( \sqrt{\alpha_{t-1}}\, x_0 + \sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot \frac{x_t - \sqrt{\alpha_t} x_0}{\sqrt{1 - \alpha_t}}, \, \sigma_t^2 I \right), \quad t > 1\]

bayes’ rule을 사용하면 forward process는 아래와 같이 바뀌고 $x_t$가 $x_{t-1}, x_0$ 에 의존하므로 더 이상 markovian이 아니게 된다. $\sigma$ 의 magnitude로 forwad process가 얼마나 stochastic한지를 조절할 수 있으며 극단적으로 $\sigma$가 0이 되면 $x_0$, $x_t$를 알면 $x_{t-1}$는 고정된 값을 가진다(deterministic).

\[q_\sigma(x_t \mid x_{t-1}, x_0) = \frac{q_\sigma(x_{t-1} \mid x_t, x_0)\, q_\sigma(x_t \mid x_0)}{q_\sigma(x_{t-1} \mid x_0)}\]

Generative process and unified variational inference objective

이제 학습 가능한 $p_\theta(x_{0:T})$를 정의하려고 한다. 각 $p_\theta^{(t)}(x_{t-1} \mid x_t)$가 $q_\sigma(x_{t-1} \mid x_t, x_0)$에 대한 지식을 활용한다. 직관적으로 noisy observation $x_t$가 주어지면 대응되는 $x_0$을 예측하고, 이를 이용하여 $q_\sigma(x_{t-1} \mid x_t, x_0)$ process를 통해 샘플 $x_{t-1}$을 얻는다. 앞서 $x_t$는 $x_t = \sqrt{\alpha_t}\, x_0 + \sqrt{1 - \alpha_t}\, \epsilon_t$로 계산할 수 있었다. 모델 $\epsilon_\theta^{(t)}(x_t)$ 는 $x_0$에 대한 정보 없이 $x_t$로부터 $\epsilon_t$를 예측하려고 시도한다. (DDPM과 마찬가지로 원본은 모르는 상태로 노이즈를 예측하겠다는 뜻이다.) $x_t$에 관한 식을 다시 쓰면 주어진 $x_t$에 대한 $x_0$의 예측인 denoised observation을 예측할 수 있다. (현재 이미지에서 예측된 노이즈를 제거하면 원본($x_0$)은 이럴 것이다 라고 추정)

\[f_\theta^{(t)}(x_t) := \frac{x_t - \sqrt{1 - \alpha_t}\,\epsilon_\theta^{(t)}(x_t)}{\sqrt{\alpha_t}}\]

Fixed prior $p_\theta(x_T) = \mathcal{N}(0, I)$에 대해 generative process 아래와 같이 정의할 수 있다.

\[p_\theta^{(t)}(x_{t-1} \mid x_t) = \begin{cases} \mathcal{N}\big(f_\theta^{(1)}(x_1), \sigma_1^2 I\big), & t = 1, \\ q_\sigma\big(x_{t-1} \mid x_t, f_\theta^{(t)}(x_t)\big), & \text{otherwise}, \end{cases}\]

여기에서 $q_\sigma\big(x_{t-1} \mid x_t, f_\theta^{(t)}(x_t)\big)$ 는 $x_0$부분을 예측값으로 대체한 것이다.

Non-Markovian process에 대한 목적함수를 다음과 같이 정의한다. (DDPM-> non-Markovian + $\sigma$가 들어간 형태)

\[J_\sigma(\epsilon_\theta) := \mathbb{E}_{x_{0:T} \sim q_\sigma(x_{0:T})} \left[ \log q_\sigma(x_{1:T} \mid x_0) - \log p_\theta(x_{0:T}) \right]\] \[= \mathbb{E}_{x_{0:T} \sim q_\sigma(x_{0:T})} \left[ \log q_\sigma(x_T \mid x_0) + \sum_{t=2}^{T} \log q_\sigma(x_{t-1} \mid x_t, x_0) - \sum_{t=1}^{T} \log p_\theta^{(t)}(x_{t-1} \mid x_t) - \log p_\theta(x_T) \right]\]

식을 보면 $\sigma$는 다른 generative process를 나타내므로 $\sigma$의 선택마다 서로 다른 모델을 학습해야 하는 것처럼 보일 수 있다. 논문에서는 $J_\sigma$는 특정한 $\gamma$에 대해 $L_{\gamma}$과 동일하다고 주장한다.

\[\textbf{Theorem 1.} \quad \text{For all } \sigma > 0,\ \text{there exists } \gamma \in \mathbb{R}_{>0}^{T} \text{ and } C \in \mathbb{R}, \text{ such that } J_\sigma = L_\gamma + C\]

정리에 대한 증명은 논문의 Appendix.B에 존재하므로 생략한다. KLD의 형태로 표현하면 다음과 같다.

\[\mathbb{E}_{x_{0:T} \sim q(x_{0:T})} \left[ \sum_{t=2}^{T} D_{\mathrm{KL}}\!\left( q_\sigma(x_{t-1} \mid x_t, x_0) \;\|\; p_\theta^{(t)}(x_{t-1} \mid x_t) \right) - \log p_\theta^{(1)}(x_0 \mid x_1) \right]\]

$L_{\gamma}$은 모델 $\epsilon^{(t)}_\theta$ 의 parameter $\theta$가 서로 다른 매개변수 t에 걸쳐 공유되지 않는다면 $\theta$에 대한 최적 해는 가중치 $\gamma$에 의존하지 않는다. (각 항을 별도로 최적화하기 때문) 이는 2가지 의미를 가지는데,

  • DDPM의 목적 함수로 $L_1$을 사용하는 것이 가능
  • 정리 1에 따르면, $J_\sigma$가 일부 $L_r$과 같기 때문에 $J_\sigma$의 최적해는 $L_1$과 동일하다.

말이 어려운데, generative process에서 말하고 싶은 것은 샘플링 방식만 DDIM으로 사용하고 학습은 DDPM의 loss를 그대로 써도 된다는 것이다.

Sampling from generalized generative process

Non-Markovian process를 위한 generative process도 $L_1$으로 학습이 가능하다. 따라서 pretrained DDPM 모델을 가져와서 쓰고 $\sigma$의 조절을 통해 적절한 샘플을 생성하는 데에 초점을 맞출 수도 있다.

이전에 살펴봤던 아래의 식을 사용하면 $x_t$로부터 $x_{t-1}$을 생성할 수 있다. $\sigma$값의 선택에 따라 같은 모델 $\epsilon_\theta^{(t)}$를 사용해도 generative process의 결과가 달라지기 때문에 재학습이 필요없다.

\[x_{t-1} = \sqrt{\alpha_{t-1}} \underbrace{ \left( \frac{x_t - \sqrt{1 - \alpha_t}\,\epsilon_\theta^{(t)}(x_t)} {\sqrt{\alpha_t}} \right) }_{\text{predicted } x_0} + \underbrace{ \sqrt{1 - \alpha_{t-1} - \sigma_t^2}\,\epsilon_\theta^{(t)}(x_t) }_{\text{direction pointing to } x_t} + \underbrace{\sigma_t \epsilon_t}_{\text{random noise}}\]

만약 $\sigma_t$가 아래와 같다면 forward process는 Markovian이 되고, generative process는 DDPM이 된다.

\[\sigma_t = \sqrt{\frac{1 - \alpha_{t-1}}{1 - \alpha_t}} \sqrt{1 - \frac{\alpha_t}{\alpha_{t-1}}}\]

모든 $t$에 대해 $\sigma_t=0$이면, forward process 는 deterministic해지고 generative process의 랜덤 노이즈의 계수가 0이 된다. 이러한 모델은 implicit probabilistic model(고정된 latent variables $x_{0:T}$로부터 샘플링)이라 한다. DDPM 목적함수로 학습한 모델이므로 DDIM이라 부른다.

그러면 실제로 어떻게 고속 샘플링을 가능하게 하는가? DDPM에서는 forward가 1000 step이면 generative도 1000step이 강제되었다. $L_1$은 특정 시점 $t$에서 marginal 분포 $q(x_t \mid x_0)$ 에만 의존하므로 모든 T단계를 거칠 필요가 없고 $T$보다 길이가 짧은 sub-sequence $\tau$를 써도 된다. 당연하게도 sub-sequence의 길이가 $T$보다 훨씬 작으면 샘플링 계산 효율이 증가할 것이다.

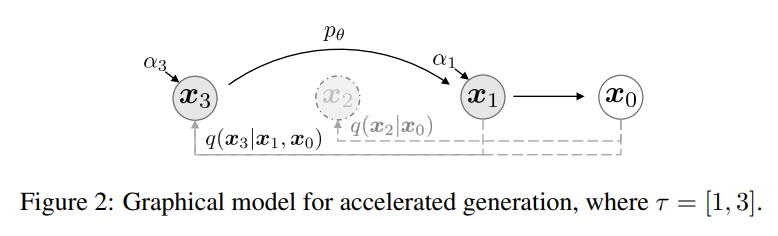
Sub-sequence sampling diagram

그림을 보면 $\tau=[1,3]$이다.

여기에서 말하고 싶은 것은 sub-sequence를 통해 빠른 샘플링이 가능하며 학습 완료 이후에는 $\sigma$ 값을 자유롭게 조절하여 stochastic DDPM ($\sigma$ 큼) / deterministic DDIM ($\sigma=0$)으로 만들 수 있다는 것이다.

아래의 식에서 $\sigma_t=0$를 넣고 $t-1$을 $t-\Delta t$로 바꿔 식을 정리하면 ODE(상미분방정식)을 풀기 위한 Euler integration과 유사해짐을 보일 수 있다.

\[x_{t-1} = \sqrt{\alpha_{t-1}} \left( \frac{x_t - \sqrt{1 - \alpha_t}\,\epsilon_\theta^{(t)}(x_t)} {\sqrt{\alpha_t}} \right) + \sqrt{1 - \alpha_{t-1} - \sigma_t^2}\,\epsilon_\theta^{(t)}(x_t) + \sigma_t \epsilon_t.\] \[\frac{x_{t-\Delta t}}{\sqrt{\alpha_{t-\Delta t}}} = \frac{x_t}{\sqrt{\alpha_t}} + \left( \sqrt{\frac{1 - \alpha_{t-\Delta t}}{\alpha_{t-\Delta t}}} - \sqrt{\frac{1 - \alpha_t}{\alpha_t}} \right) \epsilon_\theta^{(t)}(x_t)\]

ODE를 유도하기 위해 아래의 term으로 치환해보자.

\[\sqrt{\frac{1 - \alpha}{\alpha}} = \sigma, \quad \frac{x}{\sqrt{\alpha}} = \bar{x}\] \[\bar{x}_{t-\Delta t} = \bar{x}_t + (\sigma_{t-\Delta t} - \sigma_t) \epsilon_\theta^{(t)}(x_t)\]

$\alpha_{t}= \frac{1}{\sigma^2+1}$이므로

\[\bar{x}_t - \bar{x}_{t-\Delta t} = (\sigma_t - \sigma_{t-\Delta t}) \epsilon_\theta^{(t)} \left( \frac{\bar{x}_t}{\sqrt{1 + \sigma_t^2}} \right)\]

논문의 ODE 식을 얻을 수 있다.

\[d\bar{x}(t) = \epsilon_\theta^{(t)} \left( \frac{\bar{x}(t)}{\sqrt{\sigma^2 + 1}} \right) d\sigma(t)\]

Deterministic ODE trajectories를 따르면 완정된 이미지를 시작점으로 초기 노이즈 $x_T$를 찾을 수 있다는 것과 deterministic하기 때문에 interpolation이 가능하다는 것이다. 또한 저자들은 유도한 ODE식은 score-based SDE 연구와 수학적으로 동일하며, 차이점이 있는 샘플링 단계에서 작은 step으로 샘플링할 경우 DDIM방식이 $dt$가 아닌 $d\sigma(t)$에 초점을 맞추므로 유리하다라고 주장한다.

샘플링 과정 살펴보기

사실 학습은 DDPM과 동일하다. 모델도 U-Net을 사용하고 loss도 같으며 여전히 모든 timestep에 대해 랜덤 샘플링한다. 코드를 통해 DDIM 샘플링의 핵심만 살펴보자. DDIM의 코드를 차용하였다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

def sample_image(self, x, model, last=True):
    try:
        skip = self.args.skip
    except Exception:
        skip = 1

    if self.args.sample_type == "generalized":
        if self.args.skip_type == "uniform":
            skip = self.num_timesteps // self.args.timesteps
            seq = range(0, self.num_timesteps, skip)
        elif self.args.skip_type == "quad":
            seq = (
                np.linspace(
                    0, np.sqrt(self.num_timesteps * 0.8), self.args.timesteps
                )
                ** 2
            )
            seq = [int(s) for s in list(seq)]
        else:
            raise NotImplementedError
        from functions.denoising import generalized_steps

        xs = generalized_steps(x, seq, model, self.betas, eta=self.args.eta)
        x = xs
    elif self.args.sample_type == "ddpm_noisy":
        if self.args.skip_type == "uniform":
            skip = self.num_timesteps // self.args.timesteps
            seq = range(0, self.num_timesteps, skip)
        elif self.args.skip_type == "quad":
            seq = (
                np.linspace(
                    0, np.sqrt(self.num_timesteps * 0.8), self.args.timesteps
                )
                ** 2
            )
            seq = [int(s) for s in list(seq)]
        else:
            raise NotImplementedError
        from functions.denoising import ddpm_steps

        x = ddpm_steps(x, seq, model, self.betas)
    else:
        raise NotImplementedError
    if last:
        x = x[0][-1]
    return x

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import torch


def compute_alpha(beta, t):
    beta = torch.cat([torch.zeros(1).to(beta.device), beta], dim=0)
    a = (1 - beta).cumprod(dim=0).index_select(0, t + 1).view(-1, 1, 1, 1)
    return a


def generalized_steps(x, seq, model, b, **kwargs):
    with torch.no_grad():
        n = x.size(0)
        seq_next = [-1] + list(seq[:-1])
        x0_preds = []
        xs = [x]
        for i, j in zip(reversed(seq), reversed(seq_next)):
            t = (torch.ones(n) * i).to(x.device)
            next_t = (torch.ones(n) * j).to(x.device)
            at = compute_alpha(b, t.long())
            at_next = compute_alpha(b, next_t.long())
            xt = xs[-1].to('cuda')
            et = model(xt, t)
            x0_t = (xt - et * (1 - at).sqrt()) / at.sqrt()
            x0_preds.append(x0_t.to('cpu'))
            c1 = (
                kwargs.get("eta", 0) * ((1 - at / at_next) * (1 - at_next) / (1 - at)).sqrt()
            )
            c2 = ((1 - at_next) - c1 ** 2).sqrt()
            xt_next = at_next.sqrt() * x0_t + c1 * torch.randn_like(x) + c2 * et
            xs.append(xt_next.to('cpu'))

    return xs, x0_preds

random한 가우시안 노이즈에서 시작하는 것은 같고, sample_image 메서드에서 sub-sequence timestep을 생성한다.
다음으로는 샘플링 과정인 generalized_steps 메서드를 살펴보자.
seq가 [0,19,…,999]이런 오름차순을 가정하고 역순으로 샘플링되어야 하므로 뒤집어준다.
t와 next_t에 대해 alpha값을 계산한다.

i: $\tau_i$ (t시점)
j: $\tau_{i-1}$ (t-1시점)
et: 모델이 예측한 노이즈
$\sigma$는 $\eta$에 의해 조절된다. (논문 수식 16)
그리고 아래의 수식이 c1 부분에 나타나 있다.

\[\sigma_{\tau_i}(\eta) = \eta \sqrt{\frac{1 - \alpha_{\tau_{i-1}}}{1 - \alpha_{\tau_i}}} \sqrt{1 - \frac{\alpha_{\tau_i}}{\alpha_{\tau_{i-1}}}}\]

결과적으로 next step 을 구하기 위한 아래의 식을 코드로 구현한 모습이다.

\[x_{t-1} = \sqrt{\alpha_{t-1}} \left( \frac{x_t - \sqrt{1 - \alpha_t}\,\epsilon_\theta^{(t)}(x_t)} {\sqrt{\alpha_t}} \right) + \sqrt{1 - \alpha_{t-1} - \sigma_t^2}\,\epsilon_\theta^{(t)}(x_t) + \sigma_t \epsilon_t.\]

Results

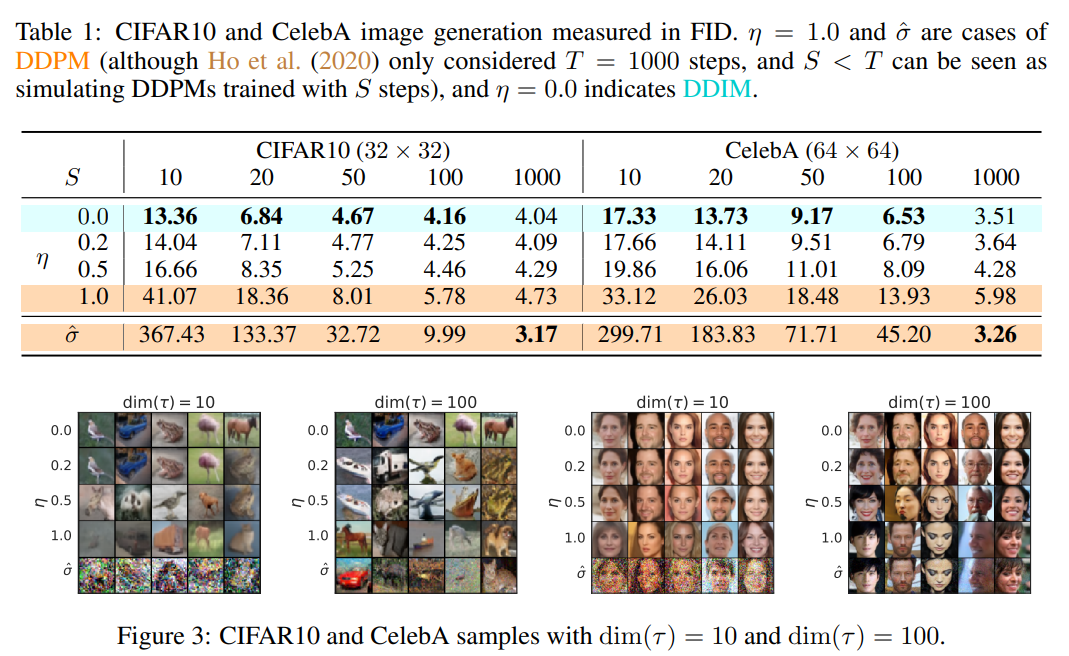
Quality comparison table

$dim(\tau)$ 가 클수록 quality가 좋아지지만 연산량 증가

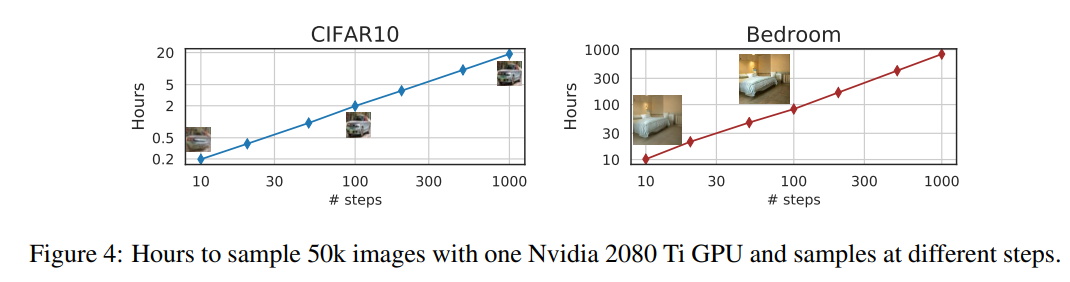
Sampling time comparison

샘플링 시간에 대한 비교

Deterministic generation trajectory

$x_0$는 initial state $x_T$에만 의존적이다. (DDIM의 generative process는 deterministic하다.) longer trajectories가 나은 quality를 보여주지만 high-level features에는 크게 영향을 미치지 않는다.

Semantic interpolation results

high-level features가 $x_T$에 인코딩되므로 DDPM과 다르게 semantic interpolation이 가능하다. 두 개의 initial $x_T$를 사용하며 변환은 spherical linear interpolation을 사용한다.

\[x_T^{(\alpha)} = \frac{\sin((1 - \alpha)\theta)}{\sin(\theta)} x_T^{(0)} + \frac{\sin(\alpha \theta)}{\sin(\theta)} x_T^{(1)}\] \[\theta = \arccos\left( \frac{(x_T^{(0)})^\top x_T^{(1)}} {\lVert x_T^{(0)} \rVert \, \lVert x_T^{(1)} \rVert} \right)\]

Reference

  • https://arxiv.org/abs/2010.02502

댓글남기기

참고

Gaussian Splatting (01) - 논문 리뷰

2 분 소요

Gaussian Splatting(GS)는 3D reconstruction의 한 분야로 3D Gaussian Splatting for Real-Time Radiance Field Rendering 논문에서 소개된 획기적인 기법이다. 해당 기법의 출시 이후 NeRF를 연구하던 연구자...

Marching Cubes 알고리즘

1 분 소요

Marching Cubes 알고리즘은 3D 공간 각 지점에서의 밀도 값을 이용하여 연속적인 표면(iso-surface)를 다각형 메쉬(보통 삼각형)로 추출하는 알고리즘이다.

Artificial Potential Field

3 분 소요

Intro Artificial Potential Field 알고리즘 (이하 APF)은 로봇의 장애물 회피에 널리 이용되는 알고리즘이다. 컨셉에 대한 이해와 활용이 어렵지 않다. 핵심은 도착점까지 이동을 시켜야 하는데 이를 위해서는 로봇의 현재 위치와 목표 위치(Goal)사이에는 인...