Denoising Diffusion Probabilistic Models(DDPM) 논문리뷰
Introduction
DDPM은 GAN, VAE기반의 이미지 생성 생태계를 diffusion기반의 생태계로 바꾼 기념비적인 논문이다. diffusion model이라는 개념은 DDPM에서 처음 나온 것은 아니고 Deep Unsupervised Learning using Nonequilibrium Thermodynamics(2015)에서 나온 개념이다.
Background

1
2
데이터 → 노이즈 추가 → 노이즈 추가 → 랜덤
데이터 ← 노이즈 제거 ← 노이즈 제거 ← 랜덤
의 구조면 diffusion model이라고 한다.
조금씩 노이즈를 추가하는 과정을 forward process(diffusion process), $q(x_t \mid x_{t-1})$
노이즈를 제거하는 과정을 reverse process $p(x_{t-1} \mid x_t)$라 한다.
diffusion에 나오는 수식을 이해하기 위해서는 bayes’ rule과
\[p(x \mid y) = \frac{p(y \mid x)\,p(x)}{p(y)} = \frac{p(x,y)}{p(y)}\]markov chain (markov 성질을 따르는 이산확률과정, t+1 상태의 확률은 t상태에만 의존) 을 알아야 한다.
\[P\!\left(x^{(t+1)} \mid x^{(0)}, \ldots, x^{(t-1)}, x^{(t)}\right) = P\!\left(x^{(t+1)} \mid x^{(t)}\right)\]Diffusion model 설명 (수식 유도 중심)
forward 프로세스에 대해 살펴보면 $t-1$ 시점에서 $t$ 시점으로 가는 변환은 미세한 값인 $\beta_{t}$ (논문에서는 T가 증가할수록 0.0001~0.02까지 선형적으로 증가)가 결합된 평균, 분산을 가지는 확률분포로 정의하고 있다.
\[q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) := \mathcal{N}\!\left(\mathbf{x}_t;\, \sqrt{1-\beta_t}\,\mathbf{x}_{t-1},\, \beta_t \mathbf{I}\right)\] \[q(\mathbf{x}_{1:T} \mid \mathbf{x}_0) := \prod_{t=1}^{T} q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\]TMI
왜 $\sqrt{1-\beta_t}\,\mathbf{x}_{t-1},\, \beta_t \mathbf{I}$ 의 형태로 정의했는지 생각해보자.
$X$가 아래와 같은 정규분포를 따른다고 할 때
\[X \sim \mathcal{N}(\mu, \sigma^2)\]샘플 $x$를 다음과 같이 정의할 수 있다.
\[x = \mu + \sigma \epsilon, \quad \epsilon \sim \mathcal{N}(0, 1)\]평균이 $\sqrt{1-\beta_t}\,\mathbf{x}_{t-1}$ ,분산이 $\beta_t \mathbf{I}$ 이므로 샘플은 아래와 같이
\[x_t = \sqrt{1 - \beta_t}\, x_{t-1} + \sqrt{\beta_t}\, \epsilon_{t-1}\]로 정의할 수 있고
샘플 $x_t$에 대해 분산을 구해보면
\[V(x_{t})=V(\sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_{t}}\epsilon_{t-1})\] \[=(\sqrt{1-\beta_t})^2V(\mathbf{x}_{t-1})+(\sqrt{\beta_{t}})^2\cdot1\]이 되고 만약 $t-1$ 시점에서 분산이 1이라면 forward 프로세스를 수행하더라도 분산을 1로 유지할 수가 있기 때문이다.
이렇게 가우시안 노이즈를 점진적으로 추가하는 과정은 markov chain이다.
diffusion process는 아래와 같이 나타낼 수도 있다.
\[\alpha_t := 1 - \beta_t \quad \text{and} \quad \bar{\alpha}_t := \prod_{s=1}^{t} \alpha_s\] \[q(x_t \mid x_0) = \mathcal{N}\!\left( x_t;\, \sqrt{\bar{\alpha}_t}\, x_0,\; (1 - \bar{\alpha}_t)\mathbf{I} \right)\]증명
TMI에서 평균과 분산이 주어졌을 때 샘플을 표현할 수 있었다.
\[x_t = \sqrt{1 - \beta_t}\, x_{t-1} + \sqrt{\beta_t}\, \epsilon_{t-1}\] \[= \sqrt{\alpha_t}\, x_{t-1} + \sqrt{1 - \alpha_t}\, \epsilon_{t-1}\] \[= \sqrt{\alpha_t}\left(\sqrt{\alpha_{t-1}}\,x_{t-2} + \sqrt{1-\alpha_{t-1}}\,\epsilon_{t-2}\right) + \sqrt{1-\alpha_t}\,\epsilon_{t-1}\] \[= \sqrt{\alpha_t \alpha_{t-1}}\,x_{t-2} + \sqrt{\alpha_t(1-\alpha_{t-1})}\,\epsilon_{t-2} + \sqrt{1-\alpha_t}\,\epsilon_{t-1}\] \[= \sqrt{\alpha_t \alpha_{t-1}}\,x_{t-2} + \sqrt{\alpha_t-\alpha_t\alpha_{t-1}}\,\epsilon_{t-2} + \sqrt{1-\alpha_t}\,\epsilon_{t-1}\]노이즈 부분의 계수를 제곱해서 더하면 $1-\alpha_{t}\alpha_{t_1}$이 된다. 즉 두개의 가우시안 노이즈항을 하나의 분산이 $1-\alpha_{t}\alpha_{t_1}$인 새로운 가우시안 노이즈로 간주할 수 있다.
\[x_t = \sqrt{\alpha_t \alpha_{t-1}}\,x_{t-2} + \sqrt{1-\alpha_t \alpha_{t-1}}\,\epsilon'_{t-2}\]처음 유도했을 때의 수식을 떠올려보자.
\[x_t = \sqrt{\alpha_t}\, x_{t-1} + \sqrt{1 - \alpha_t}\, \epsilon_{t-1}\]t-1 term을 대입하는 이 과정을 반복하면 $x_0$ 까지 갈 수 있다.
\[x_t = \sqrt{\bar{\alpha}_t}\,x_0 + \sqrt{1 - \bar{\alpha}_t}\,\epsilon'_0\] \[q(x_t \mid x_0) = \mathcal{N}\!\left( x_t;\, \sqrt{\bar{\alpha}_t}\, x_0,\; (1 - \bar{\alpha}_t)\mathbf{I} \right)\]random 가우시안 노이즈에서 어떻게 이미지를 생성할 수 있는가? 이것은 loss function과 관련이 있다.
diffusion에서는 생성모델이 $x_0$를 잘 모사하기 위해 negative log likelihood를 최소화하고자 한다. 하지만 이는 직접 계산하기 어려워 variational bound($q$라는 분포를 도입)를 사용한다. $q$를 도입하고 upper bound(ELBO)를 최소화하는 문제로 바꾸는 것이다.
\[L := \mathbb{E}\big[-\log p_\theta(x_0)\big] \le \mathbb{E}_q\left[-\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)}\right] = \mathbb{E}_q\left[-\log p(x_T) - \sum_{t \ge 1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})}\right]\]먼저 ELBO부터 살펴보자. 확률분포 적분의 형태로 나타내면 아래와 같다.
\[p_\theta(x_0) = \int p_\theta(x_{0:T}) \, dx_{1:T}\]여기에 forward 프로세스를 분모 분자에 곱해준다.
\[p_\theta(x_0) = \int q(x_{1:T}\mid x_0)\, \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \, dx_{1:T}\]기댓값의 정의에 따라 q에 대한 기댓값으로 나타낼 수 있다.
\[= \mathbb{E}_q \left[ \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \right]\]여기에 log를 씌우자.
\[\log p_\theta(x_{0}) = \log\mathbb{E}_q \left[ \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \right]\]Jensen’s inequality (Jensen 부등식)는 함수가 볼록/오목이냐에 따라 부등식의 부등호가 반대이다. log는 두번 미분했을 때 음수이므로 오목함수이고 아래의 부등식이 성립한다.
\[\mathbb{E}[g(X)] \le g(\mathbb{E}[X]) , \qquad \log \mathbb{E}[f] \ge \mathbb{E}[\log f]\]이전 기댓값 식에서 음수를 취해주면
\[-\log p_\theta(x_{0}) = -\log\mathbb{E}_q \left[ \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \right] \le \mathbb{E}_q \left[ -\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \right]\]아래의 식은 forward, reverse가 markov chain인 점을 이용하면 유도할 수 있다.
\[\mathbb{E}_q\left[-\log p(x_T) - \sum_{t \ge 1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})}\right]\]reverse에서는 t-1시점에서의 이전 상태인 t시점을 알면 되고
\[p_\theta(x_{0:T}) = p(x_T) \prod_{t=1}^{T} p_\theta(x_{t-1} \mid x_t)\]forward에서는 t시점에서의 이전 상태인 t-1시점을 알면 된다.
\[q(x_{1:T} \mid x_0) = \prod_{t=1}^{T} q(x_t \mid x_{t-1})\]로그 안의 곱 형태이므로 합 형태로 표시해준다.
\[\mathbb{E}_q\left[-\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)}\right] = \mathbb{E}_q\left[-\log p(x_T) - \sum_{t \ge 1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})}\right]\]논문에는 다음과 같이 표기할 수도 있다고 한다. 이를 유도해보자.
\[\mathbb{E}_q \Bigg[ \underbrace{D_{\mathrm{KL}}\!\left(q(x_T \mid x_0)\,\|\,p(x_T)\right)}_{L_T} + \sum_{t>1} \underbrace{D_{\mathrm{KL}}\!\left(q(x_{t-1} \mid x_t, x_0)\,\|\,p_\theta(x_{t-1} \mid x_t)\right)}_{L_{t-1}} - \underbrace{\log p_\theta(x_0 \mid x_1)}_{L_0} \Bigg]\]핵심은 loss를 KL divergence의 형태로 표시하고자 하는 것이다.
t=1일때를 분리해준다.
\[= \mathbb{E}_q \left[ -\log p(x_T) - \sum_{t>1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})} - \log \frac{p_\theta(x_0\mid x_1)}{q(x_1\mid x_0)} \right]\] \[= \mathbb{E}_q \Bigg[ - \log p(x_T) - \sum_{t>1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t, x_0)} \cdot \frac{q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)} - \log \frac{p_\theta(x_0\mid x_1)}{q(x_1\mid x_0)} \Bigg]\]바로 다음 식으로 넘어가기에는 생략된 부분이 있다. 빨간색 부분을 집중해서 보자.
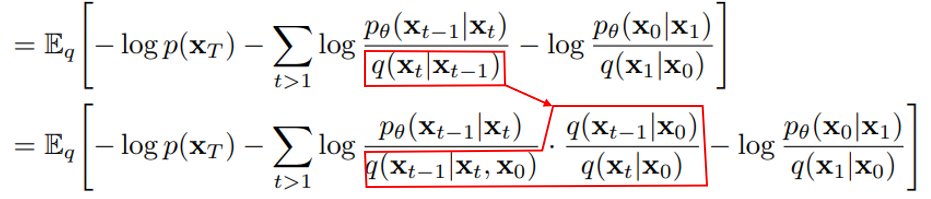
KL divergence는 같은 변수에 대한 분포의 차이이므로 같은 변수로 만들고 싶다. 여기에서 bayes’ rule을 적용하는데 forward 프로세스는 markov chain이므로 $x_0$에 대해 독립이다.
\[q(x_{t} \mid x_{t-1})=q(x_{t} \mid x_{t-1}, x_0)= \frac{q(x_t, x_{t-1}, x_0)}{q(x_{t-1}, x_{0})}\] \[\frac{q(x_t, x_{t-1}, x_0)}{q(x_{t-1}, x_{0})}= \frac{q(x_t, x_{t-1}, x_0)}{q(x_{t-1}, x_0)} \cdot \frac{q(x_t, x_0)}{q(x_t, x_0)}\]$x_t,x_0$에 대해 bayes’ rule을 역으로 적용하면
\[\frac{q(x_t, x_{t-1}, x_0)}{q(x_t, x_0)}=q(x_{t-1} \mid x_t, x_0)\]이 되고 이를 치환해주면 아래와 같은 수식으로 표현된다.
\[q(x_{t-1} \mid x_t) = q(x_{t-1} \mid x_t, x_0)\, \frac{q(x_t \mid x_0)}{q(x_{t-1} \mid x_0)}\]이를 원래 loss 식에 대입해 주면
\[= \mathbb{E}_q \Bigg[ - \log p(x_T) - \sum_{t>1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t, x_0)} \cdot \frac{q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)} - \log \frac{p_\theta(x_0\mid x_1)}{q(x_1\mid x_0)} \Bigg]\]논문에 나온 수식을 얻을 수 있다.
\[= \mathbb{E}_q \Bigg[ - \log p(x_T) - \sum_{t>1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t, x_0)} - \sum_{t>1} \log \frac{q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)} - \log \frac{p_\theta(x_0\mid x_1)}{q(x_1\mid x_0)} \Bigg]\]다음으로는 q term을 전개해보자.
\[= \mathbb{E}_q \Bigg[ - \log p(x_T) - \sum_{t>1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t, x_0)} - (\log q(x_1\mid x_0) - \log q(x_2\mid x_0) + \log q(x_2\mid x_0) - \log q(x_3\mid x_0) + \cdots) - \log \frac{p_\theta(x_0\mid x_1)}{q(x_1\mid x_0)} \Bigg]\] \[= \mathbb{E}_q \Bigg[ - \log p(x_T) - \sum_{t>1} \log \frac{p_\theta(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t, x_0)} - \log q(x_1\mid x_0) + \log q(x_t\mid x_0) - \log p_\theta(x_0\mid x_1) + \log q(x_1\mid x_0) \Bigg]\]$x_T$는 하나의 로그항으로 묶어주면 아래와 같은 수식을 얻을 수 있다.
\[= \mathbb{E}_q \left[ - \log \frac{p(x_T)}{q(x_T \mid x_0)} - \sum_{t>1} \log \frac{p_\theta(x_{t-1} \mid x_t)}{q(x_{t-1} \mid x_t, x_0)} - \log p_\theta(x_0 \mid x_1) \right]\]KL divergence를 기댓값 형태로 나타내면 아래와 같다. 위의 식을 KLD의 형태로 바꿔주면
\[D_{\mathrm{KL}}(q(z)\,\|\,p(z)) = \mathbb{E}_q \left[ \log \frac{q(z)}{p(z)} \right]\]아래와 같이 논문의 식을 유도할 수 있게 된다.
\[\mathbb{E}_q \left[ \underbrace{D_{\mathrm{KL}}\!\left(q(x_T \mid x_0)\,\|\,p(x_T)\right)}_{L_T} + \sum_{t>1} \underbrace{D_{\mathrm{KL}}\!\left(q(x_{t-1} \mid x_t, x_0)\,\|\,p_\theta(x_{t-1} \mid x_t)\right)}_{L_{t-1}} - \underbrace{\log p_\theta(x_0 \mid x_1)}_{L_0} \right]\]$L_T$는 학습에 관여하는 파라미터가 없으므로 무시한다.
$L_{t-1}$을 살펴보자.
\[p_\theta(x_{t-1} \mid x_t) = \mathcal{N}\!\big(x_{t-1};\, \mu_\theta(x_t, t),\, \Sigma_\theta(x_t, t)\big), \quad \text{for } 1 < t \le T.\]또한 논문에서는 분산을 고정했다. (KL divergence term의 목표를 두 분포의 평균을 맞추는데 더 초점을 두고 학습안정성을 위해 이렇게 가정한 것으로 보인다.)
\[\Sigma_\theta(x_t, t) = \sigma_t^2 \mathbf{I}\]여기에서 분산을 정의할 수 있는 2가지 선택지가 있다. (논문에서 두 가지 다 큰 차이가 없다고 한다.) 첫번째는 forward process의 분산인 $\beta_t$를 그대로 사용하는 것이다.
\[\sigma_t^2 = \beta_t\]아래의 두 식은 논문에서 제시하는 수식이다. 이를 유도하는 과정에서 두번째 분산이 유도된다.
\[q(x_{t-1}\mid x_t, x_0)=\mathcal{N}\!\big(x_{t-1};\,\tilde{\mu}_t(x_t,x_0),\,\tilde{\beta}_t \mathbf{I}\big)\] \[\text{where}\quad \tilde{\mu}_t=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t, \qquad \tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\,\beta_t\]두번째 분산의 형태는 다음과 같다.
\[\sigma_t^2 = \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \, \beta_t\]증명
앞서 loss 식 유도 과정에서 q/q꼴을 통해 다음과 같은 식을 얻을 수 있었다.
\[q(x_{t-1} \mid x_t) = q(x_{t-1} \mid x_t, x_0)\, \frac{q(x_t \mid x_0)}{q(x_{t-1} \mid x_0)}\]이항해준다.
\[q(x_{t-1}\mid x_t, x_0) = q(x_t \mid x_{t-1}, x_0)\, \frac{q(x_{t-1}\mid x_0)}{q(x_t \mid x_0)}\]가우시안 분포에 대한 확률밀도함수는 다음과 같이 나타낼 수 있다.
\[p(x) = \frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}} \exp\!\left( -\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu) \right)\] \[p(x) \propto \exp\!\left(-\frac{1}{2\sigma^2}(x-\mu)^2\right)\] \[q(x_{t-1}\mid x_t, x_0)\propto \exp\!\left( -\frac{1}{2} \left( \frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{\beta_t} + \frac{(x_{t-1} - \sqrt{\bar{\alpha}_{t-1}} x_0)^2}{1 - \bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\bar{\alpha}_t} x_0)^2}{1 - \bar{\alpha}_t} \right) \right)\] \[= \exp\!\left( -\frac{1}{2} \left( \frac{x_t^2 - 2\sqrt{\alpha_t}\,x_t x_{t-1} + \alpha_t x_{t-1}^2}{\beta_t} + \frac{x_{t-1}^2 - 2\sqrt{\bar{\alpha}_{t-1}}\,x_{t-1} x_0 + \bar{\alpha}_{t-1} x_0^2}{1 - \bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\bar{\alpha}_t} x_0)^2}{1 - \bar{\alpha}_t} \right) \right)\]전개하여 $x_{t-1}$에 대한 완전제곱식으로 나타내고 싶다.
\[= \exp\!\left( -\frac{1}{2} \left( \left(\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}}\right) x_{t-1}^2 - 2\left(\frac{\sqrt{\alpha_t}}{\beta_t} x_t + \frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_0\right) x_{t-1} + \cdots \right) \right)\]왜나하면
\[A x^2 - B x = A\left(x - \frac{B}{A}\right)^2 - \frac{B^2}{A}\] \[-\frac{1}{2}A\left(x_{t-1} - \frac{B}{A}\right)^2 + \text{constant}\] \[\exp\!\left(-\frac{1}{2\sigma^2}(x-\mu)^2\right)\]이 되고 지수함수 내부의 term을 각각 비교하면
\[A=\frac{1}{\tilde{\beta}_t}, \quad \tilde{\beta}_t=\frac{1}{A}, \quad \tilde{\mu}_t=\frac{B}{A}\]이 된다.
$\tilde{\beta}_t$를 먼저 계산해보자.
$\beta_t=1-\alpha_t$ 로 정의되었음을 상기하자.
또한
\[\bar{\alpha}_{t}=\alpha_t \bar{\alpha}_{t-1}\]이다(joint이므로).
\[\begin{aligned} \tilde{\beta}_t &= \frac{1}{\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}}} = \frac{\beta_t(1-\bar{\alpha}_{t-1})} {\alpha_t(1-\bar{\alpha}_{t-1}) + \beta_t} = \frac{\beta_t(1-\bar{\alpha}_{t-1})} {\alpha_t - \alpha_t \bar{\alpha}_{t-1} + \beta_t} \\ &= \frac{\beta_t(1-\bar{\alpha}_{t-1})} {\alpha_t - \alpha_t \bar{\alpha}_{t-1} + 1 - \alpha_t} = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\,\beta_t \end{aligned}\]다음은 $\tilde{\mu}_t$에 대해 계산해보자.
\[\begin{aligned}\tilde{\mu}_t(x_t, x_0) &= \left( \frac{\sqrt{\alpha_t}}{\beta_t} x_t + \frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_0 \right)\tilde{\beta}_t = \left( \frac{\sqrt{\alpha_t}}{\beta_t} x_t + \frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_0 \right) \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\,\beta_t \\ &= \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} x_t + \frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_t} x_{0}\beta_t \\ &= \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t} x_{0} + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} x_t \end{aligned}\]원래 식
\[\tilde{\mu}_t=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t\]과 동일한 형태가 됨을 확인할 수 있다.
실제 분산은 데이터 분포에 따라 달라지는데, 첫번째는 데이터의 분포가 완전 랜덤(gaussian)에 가까울 때의 최적이고 두번째는 데이터의 분포가 deterministic할때 ($x_0$ 자체가 조건부 안에서는 고정)일때 최적이다. 이미지는 두 조건 사이에 위치해 있고 논문은 두 분산의 차이가 크게 없다고 주장한다. 그러면서 조금 더 수식이 간편한 첫 번째 선택지를 택하고 있다.
\[p_\theta(x_{t-1} \mid x_t) = \mathcal{N}\!\left( x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2 \mathbf{I} \right)\] \[L_{t-1} = \mathbb{E}_q \left[ \frac{1}{2\sigma_t^2} \left\| \tilde{\mu}_t(x_t, x_0) - \mu_\theta(x_t, t) \right\|^2 \right] + C\]위의 식은 결국 KL divergence에서 $q$와 $p$의 평균을 맞추겠다는 의미이다.
증명
다변량 정규분포의 KLD는 다음과 같다. $k$:변수 차원
\[\mathrm{KL} \Big( \mathcal{N}(\mu_1, \Sigma_1) \;\|\; \mathcal{N}(\mu_2, \Sigma_2) \Big) = \frac{1}{2} \left( \operatorname{tr}(\Sigma_2^{-1} \Sigma_1) + (\mu_2 - \mu_1)^\top \Sigma_2^{-1} (\mu_2 - \mu_1) - k + \ln \frac{\det \Sigma_2}{\det \Sigma_1} \right)\] \[\Sigma_1 = \tilde{\beta}_t I, \qquad \Sigma_2 = \sigma_t^2 I, \qquad \Sigma_2^{-1} = \frac{1}{\sigma_t^2} I\]trace는 대각합이기 때문에 변수 차원인 $k$를 곱해준다.
\[\operatorname{tr}(\Sigma_2^{-1} \Sigma_1) = \operatorname{tr}\!\left( \frac{\tilde{\beta}_t}{\sigma_t^2} I \right) = k \frac{\tilde{\beta}_t}{\sigma_t^2}\]결국 trace + 공분산 2차식 + 변수 차원 + log(determinant)의 형태인데 trace가 상수이므로 우리는 공분산 2차식을 제외한 나머지는 상수이고 $\theta$가 있는 공분산 2차식에만 관심이 있다.
$\Sigma_2^{-1} = \frac{1}{\sigma_t^2} I$이므로, $(\mu_2 - \mu_1)^\top \Sigma_2^{-1} (\mu_2 - \mu_1)=\frac{1}{\sigma_t^2}\left| \mu_\theta - \tilde{\mu}_t \right|^2$ 가 되고
\[q(x_{t-1}\mid x_t, x_0)=\mathcal{N}\!\big(x_{t-1};\,\tilde{\mu}_t(x_t,x_0),\,\tilde{\beta}_t \mathbf{I}\big)\] \[p_\theta(x_{t-1} \mid x_t) = \mathcal{N}\!\left( x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2 \mathbf{I} \right)\]이므로 원래 수식의 1/2을 곱해주고 관심없는 부분은 상수 C로 처리하면
\[L_{t-1} = \mathbb{E}_q \left[ \frac{1}{2\sigma_t^2} \left\| \tilde{\mu}_t(x_t, x_0) - \mu_\theta(x_t, t) \right\|^2 \right] + C\]를 유도할 수 있다.
$\tilde{\mu}_t(x_t, x_0)$는 GT에 해당하고 forward process에서의 샘플링을 아래와 같이 도출한 바 있다.
\[x_t(x_0,\epsilon) = \sqrt{\bar{\alpha}_t}\,x_0 + \sqrt{1 - \bar{\alpha}_t}\,\epsilon'_0\] \[\tilde{\mu}_t=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t\]에 $x_0$ 을 대입해보자. (계산 편의상 $(x_0,\epsilon)$ 생략 )
\[x_t = \sqrt{\bar{\alpha}_t}\,x_0 + \sqrt{1-\bar{\alpha}_t}\,\epsilon'_0 \quad \Rightarrow \quad x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} \left(x_t - \sqrt{1-\bar{\alpha}_t}\,\epsilon_t\right)\] \[\tilde{\mu}_t= \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t} \cdot \frac{x_t - \sqrt{1-\bar{\alpha}_t}\,\epsilon_t}{\sqrt{\bar{\alpha}_t}} + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t\] \[\begin{aligned} \tilde{\mu}_t &= \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t} \cdot \frac{x_t - \sqrt{1-\bar{\alpha}_t}\,\epsilon}{\sqrt{\bar{\alpha}_t}} + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t \\ &= \left( \frac{\sqrt{\bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_t}} \frac{\beta_t}{1-\bar{\alpha}_t} + \frac{1}{\sqrt{\alpha_t}} \frac{\alpha_t(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} \right) x_t -\frac{\sqrt{\bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_t}} \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon \\ &= \frac{1}{\sqrt{\alpha_t}} \left( \frac{\beta_t+\alpha_t-\alpha_t\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\,x_t -\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon \right) \\ &= \frac{1}{\sqrt{\alpha_t}} \left( \frac{1-\alpha_t+\alpha_t-\bar{\alpha}_t}{1-\bar{\alpha}_t}\,x_t -\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon \right) \\ &= \frac{1}{\sqrt{\alpha_t}} \left( x_t(x_0,\epsilon) -\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon_t \right). \end{aligned}\]$L_{t-1}$에 대입해주면 수식을 평균에서 noise에 관한 term으로 변화시킬 수 있다.
\[L_{t-1} - C = \mathbb{E}_{x_0,\epsilon} \left[ \frac{1}{2\sigma_t^2} \left\| \frac{1}{\sqrt{\alpha_t}} \left( x_t(x_0,\epsilon) - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon \right) - \mu_\theta(x_t(x_0,\epsilon), t) \right\|^2 \right]\]loss를 최소화해야 하므로 $\mu_\theta$는 $x_t$가 주어지면(forward에서 만들어 input으로) 아래와 같은 형태를 띄어야 한다. 이 수식은 $x_t$에서 얼마나 노이즈 $\epsilon$을 파라미터화 하여 제거해야 하는지의 문제이다. ($\mu$는 $x_t,\epsilon$을 변수로 가지는 함수)
\[\mu_\theta(x,t) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\, \epsilon_{\theta}(x,t) \right)\]이를 그대로 $L_{t-1} - C$식에 대입해주면
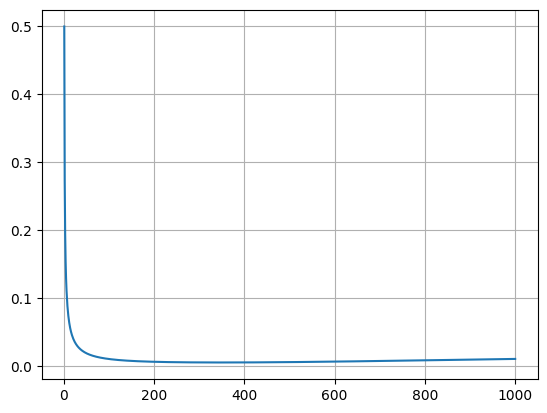
\[\mathbb{E}_{x_0,\epsilon}\left[ \frac{(1-\alpha_t)^2}{2\alpha_t(1-\bar{\alpha}_t)\,\sigma^2} \left\| \epsilon_t-\epsilon_\theta(x_t,t) \right\|^2 \right]\] \[\mathbb{E}_{x_0,\epsilon} \left[ \frac{\beta_t^2}{2\sigma_t^2 \alpha_t (1-\bar{\alpha}_t)} \left\| \epsilon - \epsilon_\theta\!\left( \sqrt{\bar{\alpha}_t}\,x_0 + \sqrt{1-\bar{\alpha}_t}\,\epsilon,\, t \right) \right\|^2 \right]\]가 된다. 계수는 무시하고 노이즈에 초점을 맞추면 단순한 형태의 loss function을 얻을 수 있다. (계수를 없앤 simplified가 성능이 더 좋았다고 한다. 계수는 t가 일정 수치 이상이면 작은 값을 가지기 때문에 denoising 부분의 weight가 약화된다. 이를 없앰으로서 denoising에 집중하게 한다.)

결과적으로 그림과 같은 알고리즘으로 학습과 샘플링을 수행할 수 있게 된다.
실제로 학습에서는 데이터를 모든 time step 에 대해 forward와 reverse를 수행하는 것은 아니고 $\alpha_t$, $\bar\alpha_t$ 를 미리 time step에 따라 정의해 놓고 random한 $t$를 뽑아서 그때 $x_0$에 노이즈를 추가해주고 이를 입력받아 모델(U-Net)은 noise를 예측한다.
$L_0$에 대해 살펴보자. $x_T$부터 $x_1$까지는 모두 실수 값을 가지는 변수들이었다. $x_1$에서 $x_0$으로 가는 과정은 $x_0$ 은 0~255의 정수 값을 가지는 (discrete) 이미지이다. (개념상 decoder에 해당) 실수형 가우시안 분포의 확률과 이산 데이터의 확률을 비교하기는 어렵기 때문에 (연속 확률에서 특정 값을 가질 확률은 0이다.) 이산적인 픽셀 확률로 바꿔주는 장치가 필요한 것이고 이것이 논문 3.3의 주 내용이다.
\[\underbrace{\log p_\theta(x_0 \mid x_1)}_{L_0}\] \[p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1) = \prod_{i=1}^{D} \int_{\delta_{-}(x_0^i)}^{\delta_{+}(x_0^i)} \mathcal{N}\!\left(x;\, \mu_\theta^i(\mathbf{x}_1,1),\, \sigma_1^2\right)\, dx\]위 식에서 i는 픽셀 인덱스, D는 픽셀 개수를 나타낸다.
이전에 reverse process를 아래와 같이 정의했었다.
\[p_\theta(x_{t-1} \mid x_t) = \mathcal{N}\!\left( x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2 \mathbf{I} \right)\]여기에 t=1을 넣고 픽셀 관점을 추가한 것이다. 이는 확률의 곱으로 표시되어 있는데 각 픽셀은 독립적인 확률을 가진다고 가정한 것이다. 모델은 $x_1$을 보고 $x_0$의 i번째 픽셀이 가질 평균을 예측해야 한다.
따라서 각 픽셀값이 가질 수 있는 범위를 정규화된 $[-1,1]$ 범위에서 $x - \frac{1}{255} \le X \le x + \frac{1}{255}$
한 픽셀이 가질수 있는 범위를 구간별로 나누어 적분하는 likelihood를 구하고자 하는 것이다. 가우시안 분포의 면적의 합은 1이 되어야 하므로 픽셀값의 극단인 -1,1에서는 각각 음의 무한대, 양의 무한대까지 적분하는 것이다.
\[\delta_{+}(x)= \begin{cases} \infty, & \text{if } x=1,\\ x+\frac{1}{255}, & \text{if } x<1, \end{cases} \qquad \delta_{-}(x)= \begin{cases} -\infty, & \text{if } x=-1,\\ x-\frac{1}{255}, & \text{if } x>-1. \end{cases}\]개념적으로는 이렇다는 것이고 적분형태의 계산이 복잡하기 때문에 실제로 학습에서 사용하지는 않는다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Training pseudo code (device등 고려안함)
beta = torch.linspace(0.0001,0.02,1000)
alpha = 1-beta
alpha_bar = torch.cumprod(alpha, dim=0)
def training_step(x_0):
"""
x_0 = (batch_size, C, H, W)
"""
# 1. t 샘플링
t = torch.randint(1, T, size=(batch_size,))
# 2. 가우시안 노이즈 샘플링
epsilon = torch.randn_like(x_0) # N(0, I)
# 3. x_t 생성
a_bar = alpha_bar[t].view(B, 1, 1, 1)
x_t = sqrt(a_bar[t]) * x_0 + sqrt(1 - a_bar[t]) * epsilon
# 4. UNet 입력 및 노이즈 예측
epsilon_pred = unet(x_t, t)
# 5. Loss 계산
loss = torch.mean((epsilon, epsilon_pred)**2)
return loss
샘플링의 경우 T 에서 1까지 반복문을 수행하는데 만약 t>1이면 노이즈를 추가해 준다. 여기에서는 2가지 분산 선택지 중 2번 분산($\tilde{\beta}$)을 선택한다. 이렇게 함으로써 샘플의 다양성을 높일 수 있다. (stochastic한 term DDIM논문은 deterministic)
논문에서는 $t = T \rightarrow 1$로 반복하고 $T>1$ 인 경우에 노이즈를 추가하지만
실제 구현은 $t = T-1 \rightarrow 0$로 반복하고 $T>0$ 인 경우에 노이즈를 추가한다.
이때 코드의 t=0 step 입력은 논문상의 $x_1$에 해당하고 출력이 최종 $x_0$이다.
(TMI: 원 논문의 구현은 posterior variance추가에서 log0을 방지하기 위해 1e-20의 하한을 둔다.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Inference pseudo code
alpha_bar_prev = F.pad(alpha_bar[:-1], (1, 0), value=1.0) # alpha_bar_{t-1}
posterior_variance = beta * (1. - alpha_bar_prev) / (1. - alpha_bar) # tilde beta
def sampling():
# 1. 가우시안 노이즈에서 시작
x_T = torch.randn((batch_size, C, H, W)) # N(0, I)
x = x_T
for t in reversed(range(0, T)):
# 2. 노이즈 예측
epsilon_pred = unet(x, t)
# 3. x_{t-1} 계산
x = (1/sqrt(alpha[t])) * (x - (beta[t]/sqrt(1-alpha_bar[t])) * epsilon_pred)
# 4. 노이즈 추가 (t>0일 때만, 논문알고리즘상 t>1의 의미)
if t > 0:
z = torch.randn_like(x)
x = x + sqrt(posterior_variance[t]) * z
return x # x_0
U-Net model
간단하게 표현하긴 했고 최소한의 구현만으로도 diffusion model은 동작하지만 원 논문의 diffusion model의 학습 코드는 성능을 올리기 위한 여러 디테일들이 결합되어 있다. 이는 코드를 직접 참고하는 것이 좋다.
모델의 아키텍쳐는 U-Net인데 based는 PixelCNN++의 backbone에 기반한다. 크게 다른 점은 time embedding과 self-attention이다.
transformer의 sinusoidal position embedding을 time step에 적용하여 모델에 지금 노이즈가 얼마나 섞여 있는지를 간접적으로 알려준다.
1
2
3
4
5
6
# Timestep embedding
with tf.variable_scope('temb'):
temb = nn.get_timestep_embedding(t, ch)
temb = nn.dense(temb, name='dense0', num_units=ch * 4)
temb = nn.dense(nonlinearity(temb), name='dense1', num_units=ch * 4)
assert temb.shape == [B, ch * 4]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def resnet_block(x, *, temb, name, out_ch=None, conv_shortcut=False, dropout):
B, H, W, C = x.shape
if out_ch is None:
out_ch = C
with tf.variable_scope(name):
h = x
h = nonlinearity(normalize(h, temb=temb, name='norm1'))
h = nn.conv2d(h, name='conv1', num_units=out_ch)
# add in timestep embedding
h += nn.dense(nonlinearity(temb), name='temb_proj', num_units=out_ch)[:, None, None, :]
h = nonlinearity(normalize(h, temb=temb, name='norm2'))
h = tf.nn.dropout(h, rate=dropout)
h = nn.conv2d(h, name='conv2', num_units=out_ch, init_scale=0.)
if C != out_ch:
if conv_shortcut:
x = nn.conv2d(x, name='conv_shortcut', num_units=out_ch)
else:
x = nn.nin(x, name='nin_shortcut', num_units=out_ch)
assert x.shape == h.shape
print('{}: x={} temb={}'.format(tf.get_default_graph().get_name_scope(), x.shape, temb.shape))
return x + h
원 논문은 tensorflow로 구현되어 있는데 ch에 곱해진 4는 hyperparameter이다. resnet_block안에서 (B,H,W,C) 에 (B,1,1,C)가 broadcasting되어 그대로 element-wise하게 더해진다. (느낌적으로는 bias와 유사하다) (TMI: resnet_block은 U-Net모델의 downsampling, upsampling의 기본 단위 모듈이다)
다음은 self-attention 부분인데 tensorflow의 nn.nin은 torch의 nn.Conv2d(c,c,kernel_size=1)과 동일하며 1x1 convolution이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def attn_block(x, *, name, temb):
B, H, W, C = x.shape
with tf.variable_scope(name):
h = normalize(x, temb=temb, name='norm')
q = nn.nin(h, name='q', num_units=C)
k = nn.nin(h, name='k', num_units=C)
v = nn.nin(h, name='v', num_units=C)
w = tf.einsum('bhwc,bHWc->bhwHW', q, k) * (int(C) ** (-0.5))
w = tf.reshape(w, [B, H, W, H * W])
w = tf.nn.softmax(w, -1)
w = tf.reshape(w, [B, H, W, H, W])
h = tf.einsum('bhwHW,bHWc->bhwc', w, v)
h = nn.nin(h, name='proj_out', num_units=C, init_scale=0.)
assert h.shape == x.shape
print(tf.get_default_graph().get_name_scope(), x.shape)
return x + h
self-attention 공식대로 w에서 (h,w)에서 HxW개 위치에 대한 attention 확률분포를 구하고 h에서 가중평균하여 (b,h,w,c)의 shape으로 만든다. 그대로 입력인 x에 더해줘서 전체 이미지의 문맥 정보를 더해준다의 의미로 해석하면 좋다. 논문에서는 feature map이 16x16 때 attention을 수행했다고 언급한다.
Results
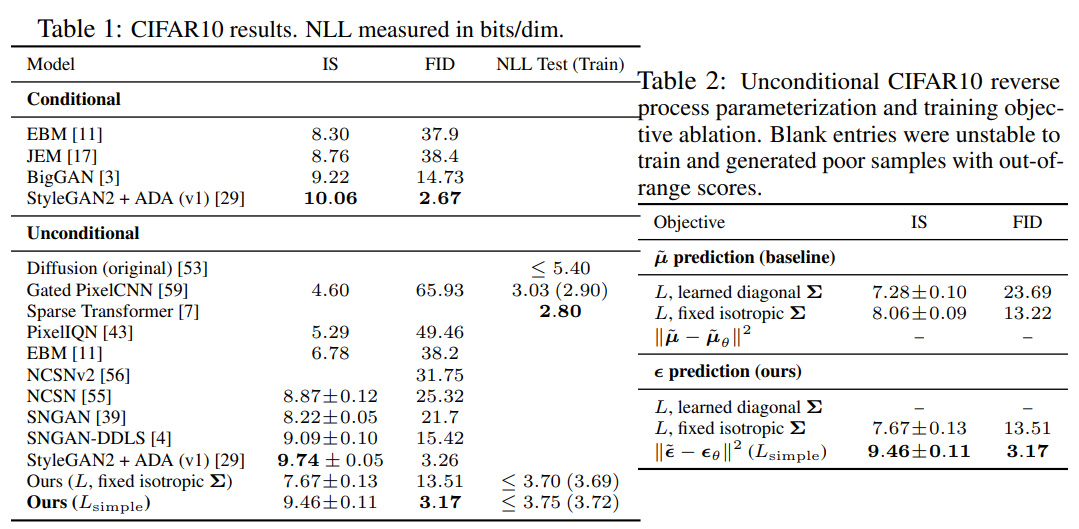
실험결과 noise를 예측하게 함으로써 성능 개선과 함께 다른 생성형 모델과 견줄만한 성능을 보여주고 있다. ($\mu$에 비해 $\mathcal{N}!\left(0, \mathbf{I}\right)$의 가우시안 노이즈를 예측하는 문제가 간단하다.)

Reference
- https://arxiv.org/abs/2006.11239
- https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
- https://cvpr2022-tutorial-diffusion-models.github.io/
댓글남기기