ROS2-005. Turtlesim 03 - 좌표계

축	위치(선속도 linear)	회전(각속도 angular)
x	거북이 몸 전방(앞/뒤) 방향 속도	—
y	몸 좌(＋)/우(－) 측방(“미끄러지기”) 속도	—
z	—	몸 위에서 내려다본 시계반대(＋)·시계(－) 회전 속도

평면 강체 운동에서 속도 벡터 v 와 각속도 ω(= angular.z) 사이에는

$v = \omega \times r$

$\omega$=(0,0,$\omega$), $r$=$(r_{x},r_{y},0)$

가 성립.

여기서 r 은 순간 회전 중심(ICR)에서 몸체 방향으로의 벡터 (반대로 봐도 되지만, 부호에 -를 해줘야 한다)

몸 좌표계에서

$v_{x}=−\omega r_{y},$ $v_{y}=\omega r_{x}$

따라서

$\displaystyle r_{x} = \frac{v_{y}}{\omega}$, $\displaystyle r_{y} = -\frac{v_{x}}{\omega}$

\[R = \| \mathbf{r} \| = \frac{\sqrt{v_x^2 + v_y^2}}{|\omega|}\]

• R : 궤적 원의 반지름
• $v_{x}$ = linear.x, $v_{y}$ = linear.y
• ω = angular.z (라디안 / 초)

ros2 topic pub --once /turtle1/cmd_vel geometry_msgs/msg/Twist "{linear: {x: 2.0, y: 0.0, z: 0.0}, angular: {x: 0.0, y: 0.0, z: 0.0}}"
ros2 topic pub --rate 1 /turtle1/cmd_vel geometry_msgs/msg/Twist "{linear: {x: 0.0, y: 1.0, z: 0.0}, angular: {x: 0.0, y: 0.0, z: 1.0}}"
ros2 topic pub --rate 1 /turtle1/cmd_vel geometry_msgs/msg/Twist "{linear: {x: 0.0, y: 1.0, z: 0.0}, angular: {x: 0.0, y: 0.0, z: 3.14}}"
ros2 topic pub --rate 1 /turtle1/cmd_vel geometry_msgs/msg/Twist "{linear: {x: 0.0.1, y: 1.0, z: 0.0}, angular: {x: 0.0, y: 0.0, z: 3.14}}"
ros2 topic pub --rate 1 /turtle1/cmd_vel geometry_msgs/msg/Twist "{linear: {x: 0.1, y: 1.0, z: 0.0}, angular: {x: 0.0, y: 0.0, z: 3.14}}"
ros2 topic pub --rate 1 /turtle1/cmd_vel geometry_msgs/msg/Twist "{linear: {x: 0.0, y: 1.0, z: 0.0}, angular: {x: 0.0, y: 0.0, z: 1.5}}"

linear (x, y)	angular.z	속도 크기 $\sqrt{x^{2}+y^{2}}$​	반지름 R
(0, 1)	1.0	1	1 / 1 = 1.00
(0, 1)	3.14 ≈ π	1	1 / π ≈ 0.32
(0.1, 1)	3.14	√(1.01) ≈ 1.005	1.005 / π ≈ 0.32
(0, 1)	1.5	1	1 / 1.5 ≈ 0.67

ros2 topic pub --rate 1 /turtle1/cmd_vel geometry_msgs/msg/Twist "{linear: {x: 2.0, y: 1.0, z: 0.0}, angular: {x: 0.0, y: 0.0, z: 1.0}}"

만약 해당 명령을 실행했을 때 회전 중심은 시작 위치로 얼마나 떨어져 있을까?

rx = vy/w, ry = -vx/w 이므로 rx = 1, ry = -2가 된다.

거북이 현재 자세를 $(x_{0},y_{0},\theta_{0})$ 이라고 했을 때 몸 -> 월드 변환은 회전 행렬

\[R(\theta_0) = \begin{bmatrix} \cos \theta_0 & \sin \theta_0 \\ - \sin \theta_0 & \cos \theta_0 \end{bmatrix}\]

이므로

\[\begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix} = \begin{bmatrix} \cos \theta_0 & -\sin \theta_0 \\ \sin \theta_0 & \cos \theta_0 \end{bmatrix} \begin{bmatrix} r_x \\ r_y \end{bmatrix}\]

가 된다. 좌표 벡터를 반시계 방향으로 회전시켰을 때의 위치 변화량을 나타내는 것이다.

전개하면,

\[\Delta x = \cos \theta_0 \cdot r_x - \sin \theta_0 \cdot r_y\] \[\Delta y = \sin \theta_0 \cdot r_x + \cos \theta_0 \cdot r_y\]

벡터 $r$은 ICR -> 거북이 이므로

\[x_{ICR} = x_{0} - \Delta x\] \[y_{ICR} = y_{0} - \Delta y\]

$\Delta x=1$, $\Delta y=-2$가 되므로 회전 중심은 월드좌표계 초기 거북이 위치로부터 (-1,2) 이동한 곳이다.

rqt_graph

rqt_graph는 GUI를 통해 토픽과 노드의 관계를 시각화한다. 동그라미는 노드이며 사각형은 토픽이다.

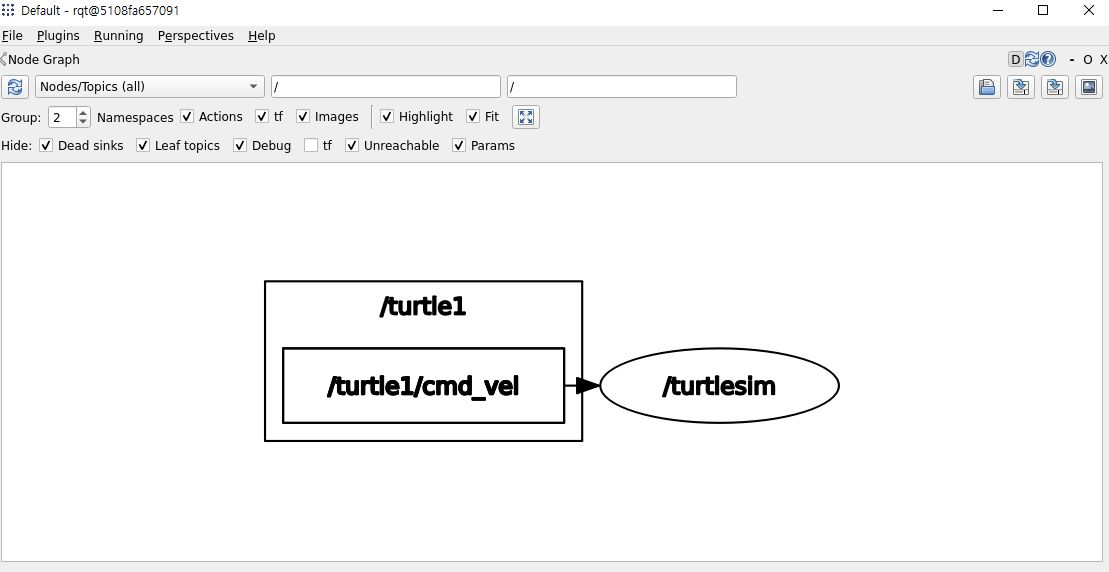
그림을 보면, /turtle1/cmd_vel 토픽을 발행하고 /turtlesim 노드가 이를 구독하고 있다.