Artificial Potential Field

Intro

Artificial Potential Field 알고리즘 (이하 APF)은 로봇의 장애물 회피에 널리 이용되는 알고리즘이다. 컨셉에 대한 이해와 활용이 어렵지 않다. 핵심은 도착점까지 이동을 시켜야 하는데 이를 위해서는 로봇의 현재 위치와 목표 위치(Goal)사이에는 인력(Attractive Force)을 발생시키고 로봇의 현재 위치와 장애물의 위치 사이에는 척력(Repulsive Force)를 발생시켜 인력과 척력의 합 벡터로 이동하는 경로를 생성하고자 하는 것이다.

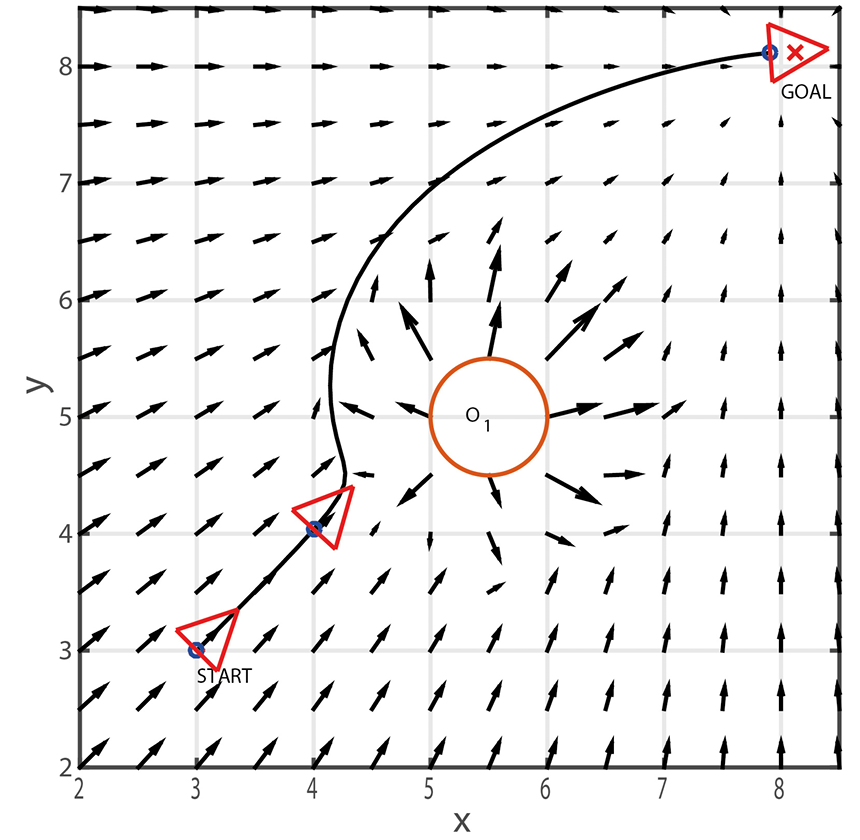
Attractive Force

Attractive Force는 Goal이 로봇을 끌어당기는 힘이다. 로봇의 현재 위치를 $M(x, y)$, 목표 위치를 $G(x_g, y_g)$ 라 하면 로봇의 상태를 벡터 $q = [x, y]^T$ 로 표현할 수 있다. $\rho$는 유클리드 거리로 두면 다음과 같은 식이 성립한다.

\[\rho_{goal}(q) = \| M(x, y) - G(x_g, y_g) \|_2\]

Attractive potential energy를 다음과 같이 정의한다. \(U_{\text{att}}(q) = \frac{1}{2}k_{\text{att}} \| q - q_{\text{goal}} \|\)

이 식은 스프링 탄성 에너지 식과 비슷한데 목적지까지 가고자 하는 힘이 목적지에 멀수록 그 에너지가 크다 이런 느낌으로 이해하면 편하다. 엄밀한 정의라기보다는 컨셉에 맞게 수학적으로 근사한 모델이라고 보면 될 것 같다. 힘은 potential energy가 감소하는 방향으로 작용하기 때문에(정의가 그렇다) $U_{\text{att}}(q)$ 를 $q$에 대해 미분하게 되면 \(\mathbf{F}_{\text{att}}(q) = - \nabla U_{\text{att}}(q)\) \(\mathbf{F}_{\text{att}}(q) = -k \big( M(x,y) - G(x_g, y_g) \big) = k \big( G(x_g, y_g) - M(x,y) \big)\) 가 된다. 즉 goal이 끌어당기는 힘은 goal과 현재 로봇의 위치가 멀수록 커지는 것이다.

Repulsive Force

Repulsive Force는 장애물이 로봇을 밀어내는 힘이다. 장애물과 로봇의 거리를 아래와 같이 정의할 수 있다. \(\rho(q) = \| O(x_o, y_o) - M(x, y) \|_2\)

Repulsive potential energy는 다음과 같이 정의한다. 이건 개념적으로 로봇이 가고 싶지 않은 곳을 높은 언덕으로 만드는 가상 에너지의 느낌이다. 대신에 가까울수록 에너지가 커져야 하므로 거리의 역수를 사용한다. 여기에서 $\rho_0$는 장애물의 영향 범위이다. 장애물의 영향권 밖에 로봇이 있으면 굳이 힘을 받을 필요가 없다. \(U_{\text{rep}}(q) = \begin{cases} \frac{1}{2}k_{rep} \left( \frac{1}{\rho(q)} - \frac{1}{\rho_0} \right)^2 & \text{if } \rho(q) \le \rho_0 \\[6pt] 0 & \text{if } \rho(q) > \rho_0 \end{cases}\)

마찬가지로 힘의 방향은 탄성 에너지가 감소하는 방향이므로 $q$에 대해 미분하면 \(\mathbf{F}_{\text{rep}}(q) = - \nabla U_{\text{rep}}(q)\) \(\nabla U_{\text{rep}}(q) = \begin{cases} -k_{rep} \left( \frac{1}{\rho(q)} - \frac{1}{\rho_0} \right) \frac{1}{\rho^2(q)} \nabla \rho(q) & \text{if } \rho(q) \le \rho_0 \\[6pt] \mathbf{0} & \text{if } \rho(q) > \rho_0 \end{cases}\)

최종적으로 Repulsive Force는 아래와 같이 된다. \(\mathbf{F}_{\text{rep}}(q) = \begin{cases} k_{rep} \left( \frac{1}{\rho(q)} - \frac{1}{\rho_0} \right) \frac{1}{\rho^2(q)} \nabla \rho(q) & \text{if } \rho(q) \le \rho_0 \\[6pt] \mathbf{0} & \text{if } \rho(q) > \rho_0 \end{cases}\)

파이썬으로 구현하면 다음과 같다.

class APF:
    def __init__(self, K_attractive=0.02, K_repulsive=3.0, obstacle_range=5):
        self.K_att = K_attractive
        self.K_rep = K_repulsive
        self.obs_range = obstacle_range

    def calculate_attractive_force(self, pos_robot, pos_goal):
        robot2goal = np.array(pos_goal) - np.array(pos_robot)
        distance = np.linalg.norm(robot2goal)
        if distance == 0:
            return np.array([0, 0])

        F_attractive = self.K_att * robot2goal

        return F_attractive

    def calculate_repulsive_force(self, pos_robot, obstacles):
        total_repulsive_force = np.array([0,0], dtype=float)
        for obstacle in obstacles:
            robot2obs = np.array(obstacle) - np.array(pos_robot)
            distance = np.linalg.norm(robot2obs)

            if distance < self.obs_range and distance > 0:
                robot2obs_unit = robot2obs/distance
                # F_rep = K_rep * (1/distance - 1/obs_range) * (1/d^2) * (-unit vector) : 장애물 반대방향으로 힘이 적용되어야 함
                repulsive_magnitude = self.K_rep*(1/distance - 1/self.obs_range)*(1/(distance**2))
                F_repulsive = -repulsive_magnitude*robot2obs_unit
                total_repulsive_force += F_repulsive

        return total_repulsive_force

    def calculate_total_force(self, pos_robot, pos_goal, obstacles):
        F_att = self.calculate_attractive_force(pos_robot, pos_goal)
        F_rep = self.calculate_repulsive_force(pos_robot, obstacles)
        return F_att + F_rep

간단한 알고리즘이지만 실제로도 잘 동작하기에 널리 이용된다. 실제로 테스트하면서 계수(K_attractive, K_repulsive)를 조절하기만 하면 된다. 다만 이를 그대로 로봇에 적용하면 안된다. 여기에서는 로봇과 장애물은 점이라고 가정했지만 실제로는 로봇과 장애물은 크기를 가지고 있기 때문에 이를 고려해야 한다. 또한 실제 상황에서는 로봇의 최대 속도가 정해져 있기 때문에 이를 고려하여 이동하고 상태를 업데이트해 줄 필요가 있다. 단점으로는 APF는 장애물이 밀어내는 힘과 목표 지점이 끌어당기는 힘이 평형을 이룰 경우 local minima에 빠질 수 있다. 이를 방지하기 위해 tangential force (장애물을 원형으로 돌아가는 힘)을 적용해 볼 수 있다.

시뮬레이션 코드는 https://github.com/soribido/Geometry-Aware-Robotics/blob/main/obstacle_avoidance/APF_improved.py에서 확인할 수 있으며
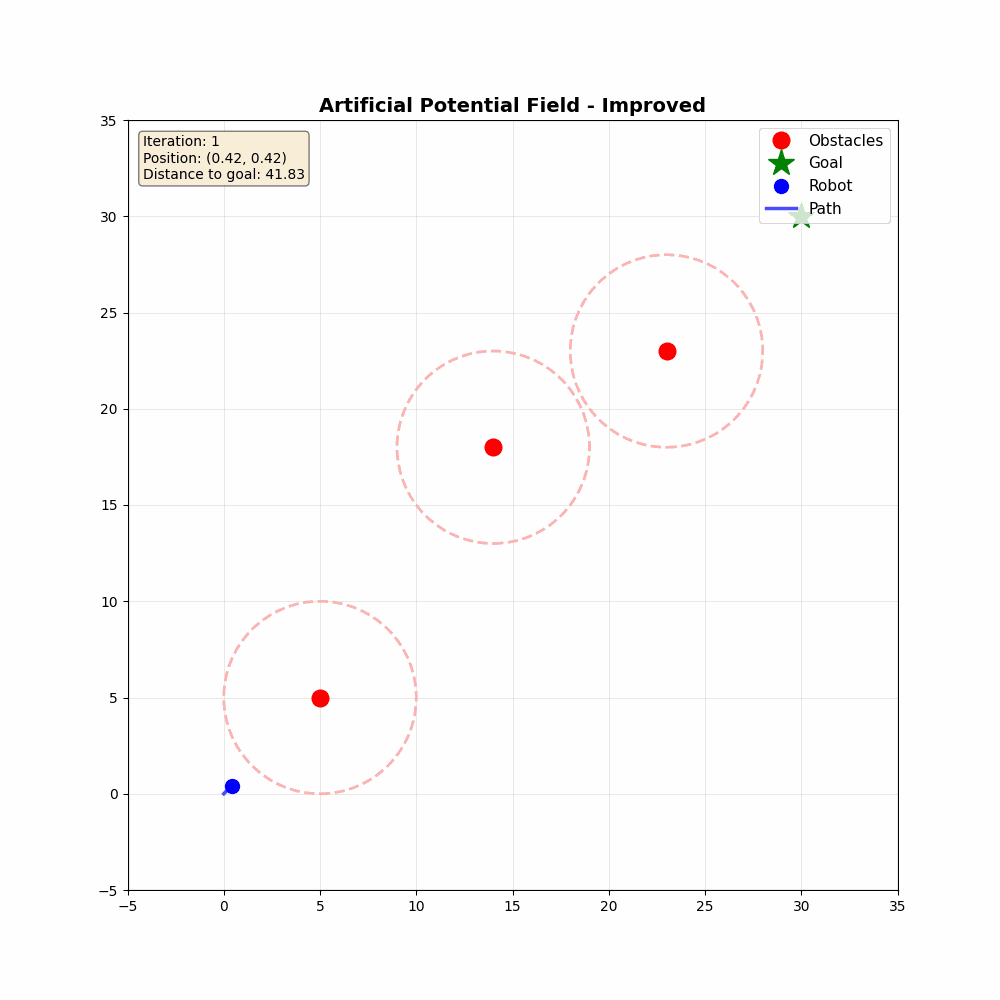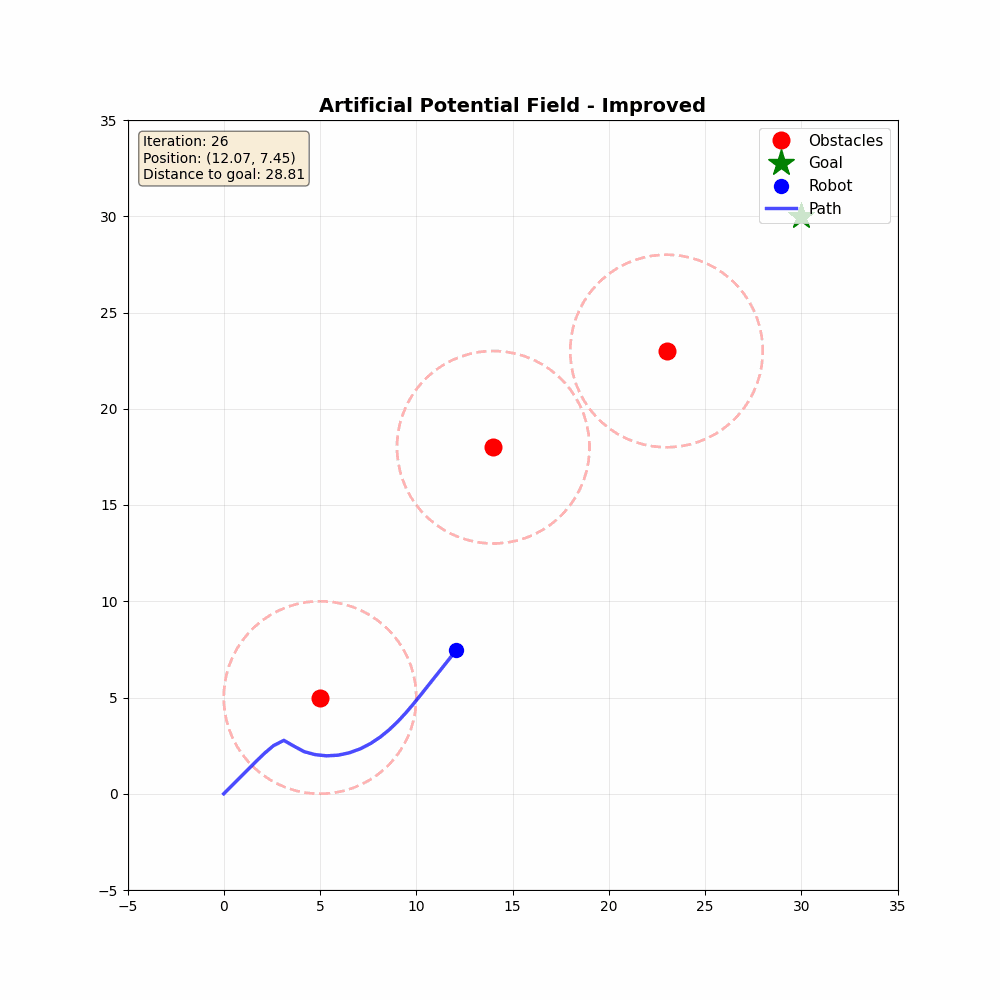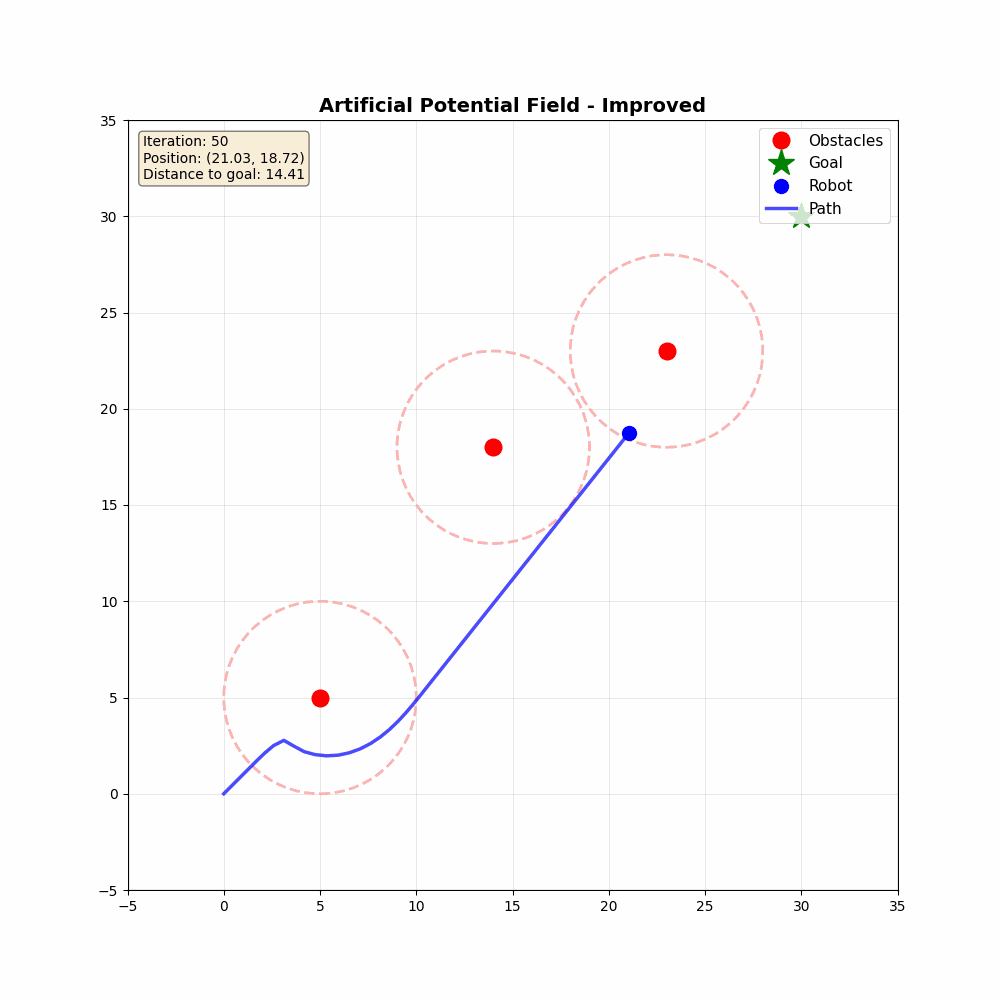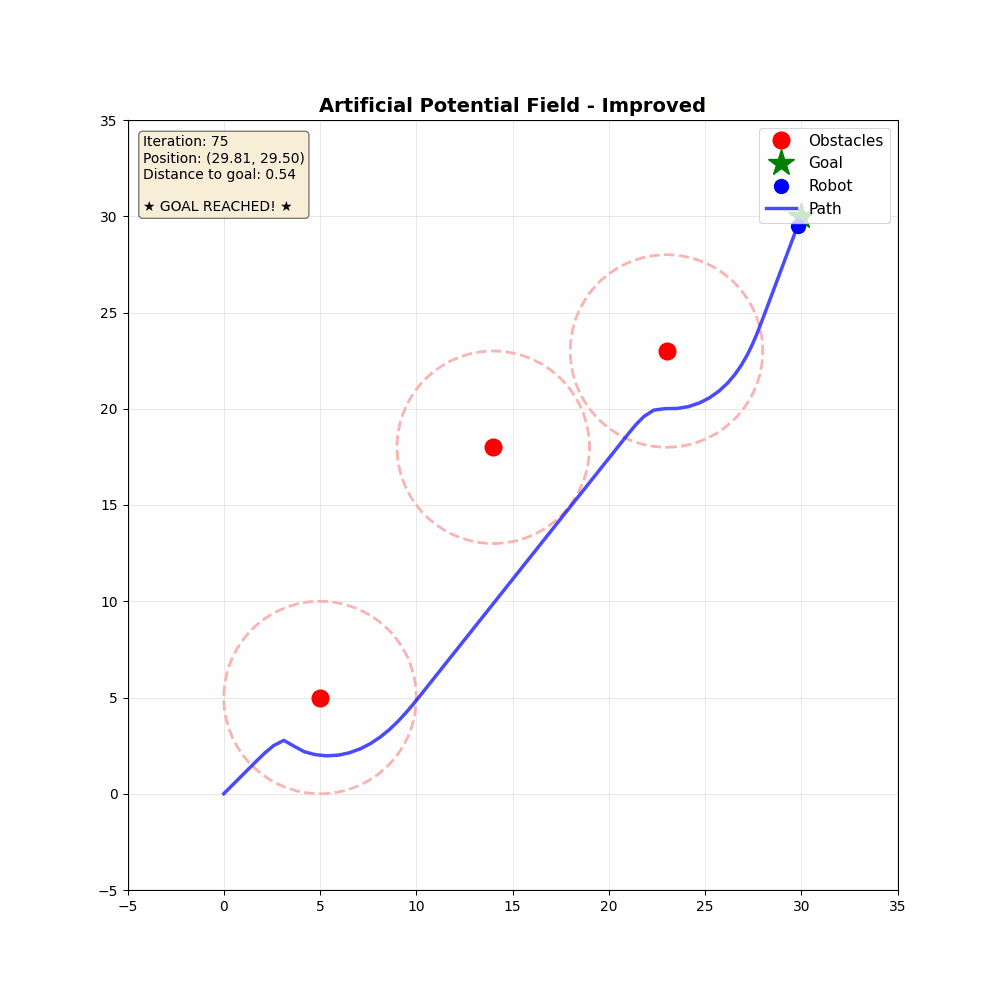
결과적으로는 아래와 같은 시뮬레이션 결과물을 얻을 수 있다.

Reference

• Khatib, Oussama. “Real-time obstacle avoidance for manipulators and mobile robots.” The international journal of robotics research 5.1 (1986): 90-98.
• Fedele, Giuseppe, et al. “Obstacles avoidance based on switching potential functions.” Journal of Intelligent & Robotic Systems 90.3 (2018): 387-405.